[ｽﾃｯﾌﾟ問題1] 次文の(ア)～(ク)に最も適した数と式を入れなさい。
銅酸化物の組成式CuXOY において, XとYの数値は下図の結晶の単位格子から次のようにして決められる。ひとつの原子の割合は完全に格子内に存在するとき (ア)とすると,
(1)単位格子の隅にある酸素原子が格子内にどのくらいの割合で存在するかを考える。
(2)隅以外の各原子は格子内にどのくらいの割合で存在するかを考える。
(3)銅原子の総和の割合と酸素原子の総和の割合の整数比を考える。
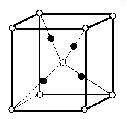(image0)(1)では, ひとつの隅の酸素原子は格子内に(イ)存在するから全ての隅の割合は(ウ)となる。(2)では, 酸素原子は (エ), 銅原子は (オ)となる。(3)では, 銅原子の場合は (カ), 酸素原子は (キ)となる。 よって単位格子内の銅と酸素の原子の割合の整数比は
X：Y = (ク)
答は
(ア)2(イ)1/4(ウ)(1/4)×8 = 2(エ)1(オ)1×4 = 4(カ)4(キ)2 + 1 = 3(ク)4：3
(ア)1(イ)1/8(ウ)(1/8)×8 = 1(エ)1(オ)1×4 = 4(カ)4(キ)1 + 1 = 2(ク)4：2
(ア)1(イ)1/4(ウ)(1/4)×8 = 2(エ)1(オ)1×2 = 2(カ)2(キ)2 + 1 = 3(ク)2：3
(ア)1(イ)1/8(ウ)(1/8)×8 = 1(エ)1(オ)1×4 = 4(カ)4(キ)1 + 1 = 2(ク)2：1
[ｽﾃｯﾌﾟ問題2] 次文の(ア)～(サ)に最も適した数を入れなさい。計算のために必要があれば次の値を用いてよい。原子量：酸素16.0, 銅63.6, ｱﾎﾞｶﾞﾄﾞﾛ数6.02×1023.
結晶酸化銅(I)の単位格子は下図のとおりである。３本の結晶軸の長さはいずれも 4.27 × 10-8 cmで, 黒丸は銅原子の中心を, 白丸は酸素原子の中心を表わす。
(image0)この単位格子から, 結晶酸化銅(I)の密度g/cm3は次のようにして求められる。
(1)単位格子の体積を求める。(2)単位格子内の各原子の質量を原子量とｱﾎﾞｶﾞﾄﾞﾛ数から求める。(3)単位格子の質量を(2)から求めて(1)の体積で割る。
(1)で, 単位格子の体積は (ア) = (イ)cm3
(2)で, 銅原子は(ウ)個存在するから {(エ)/(オ)} × (ウ) = (カ)g 酸素原子は(キ)個存在するから {(ク)/(オ)} × (キ) = (ケ)g
(3)で, (2)から求まる単位格子の質量：(カ)+(ケ) = (コ)g と (1)の単位格子の体積：(イ)cm3から結晶酸化銅(I)の密度は (コ)/(イ) = (サ)g/cm3
答は
(ア)(4.27 × 10-8)3(イ)7.785 × 10-24(ウ)2(エ)63.6(オ)6.02×1023(カ)2.113×10-23(キ)4(ク)16.0(ケ)10.632 ×10-23(コ)12.745×10-23(サ)1.64
(ア)(4.27 × 10-8)3(イ)7.785 × 10-23(ウ)4(エ)63.6(オ)6.02×1023(カ)4.226×10-22(キ)2(ク)16.0(ケ)5.316 ×10-23(コ)47.58×10-23(サ)6.11
(ア)(4.72 × 10-8)3(イ)1.052 × 10-22(ウ)4(エ)63.6(オ)6.02×1023(カ)4.226×10-22(キ)2(ク)16.0(ケ)5.316 ×10-23(コ)47.58×10-23(サ)4.52
(ア)(4.27 × 10-8)3(イ)7.785 × 10-24(ウ)4(エ)63.6(オ)6.02×1023(カ)4.226×10-23(キ)2(ク)16.0(ケ)5.316 ×10-23(コ)9.547×10-23(サ)1.23
[ｽﾃｯﾌﾟ問題3] 次文の(ア)～(キ)に最も適した語句と数を入れなさい。
結晶酸化銅(I)の単位格子は図 I のようになる。結晶は単位格子の(ア)なので, 単位格子を図 I 中の酸素原子(○)に注目していくつかを重ねてみると図 II になる。
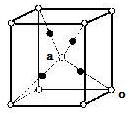
図I (image16-1)
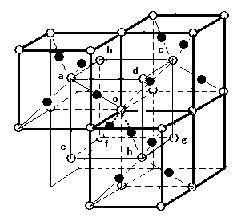
図 II (image16-2)
図 II に示されているように, a の酸素原子を中心とした立方体を a → o にそって並進移動させた後, a―o軸を回転軸として180°回転させると, 立方体abcdefghとなり, いくつかの単位格子を積み重ねた元の図IIと完全に(イ)。
このことは, 図 I では(ウ)の位置の o の酸素原子がabcdefghの立方体の(エ)となり, 最短距離の(オ)つの銅原子に取り囲まれている。
いいかえるならば, 図 I において, 酸素原子の o の周りには, 銅原子が全て(カ)が, o と a は(キ)で, o も (オ)つの銅原子に取り囲まれており, また結晶中の全ての酸素原子にも適合することを意味する。
答は
(ア)積み重ね(イ)重なる(ウ)隅(エ)中心(オ)4(カ)示されている(キ)同等の状態
(ア)積み重ね(イ)重なる(ウ)中心(エ)隅(オ)4(カ)示されていない(キ)違った状態
(ア)積み崩し(イ)重ならない(ウ)隅(エ)中心(オ)2(カ)示されている(キ)違った状態
(ア)積み重ね(イ)重なる(ウ)隅(エ)中心(オ)4(カ)示されていない(キ)同等の状態
[ｽﾃｯﾌﾟ問題4] 次文の(ア)～(エ)に最も適した語句と数を入れなさい。
結晶の酸化銅(I)の単位格子は下図のようになる。3本の結晶軸の長さはいずれも 4.27 × 10-8 cmで, 黒丸は銅原子の中心を, 白丸は酸素原子の中心を表わす。酸素原子は(ア)格子をつくっており, 銅原子は立方体の中心と隅を結ぶ線上の真中に位置している。
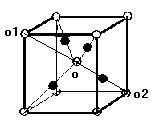
上図から, 銅原子半径を rCU, 酸素原子半径をrO, o1―02の長さを a とすると,
a = (イ)×(rCU + rO) …①
また, 結晶軸の長さは4.27 × 10-8 cm なので
a2 = (4.27 × 10-8)2×(ウ) …②
よって, 銅原子半径 rCU は, 酸素原子半径を7.40×10-9cmとすると, ①と②から
rCU = (エ) × 10-8cm
答は
(ア)単純立方(イ)2(ウ)2(エ)2.28
(ア)体心立方(イ)4(ウ)3(エ)1.11
(ア)体心正方(イ)4(ウ)3(エ)1.11
(ア)面心立方(イ)4(ウ)4(エ)1.40