[ステップ問題1]の解答・・・(ア)1(イ)1/8(ウ)(1/8)×8 = 1(エ)1(オ)1×4 = 4(カ)4
(キ)1 + 1 = 2(ク)2：1
ﾋﾝﾄ
●単体の金属結晶は, 主として次の三つの構造がある。
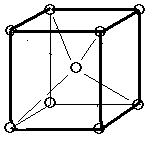
(1)体心立方格子 image1・・・配位数：8, 格子内原子数：2, 格子内原子体積占有率：68%, 例 K, Ba, Ra, V, Nb, Ta, W (配位数：注目原子を取り巻く最も近い他の原子の数を意味する)
(2)面心立方格子 image2・・・配位数：12, 格子内原子数：4, 格子内原子体積占有率：74%, 例 Al, Pd, Pt, Cu, Ag, Au, Pb
(3)六方最密構造 image6・・・配位数：12, 格子内原子数：6, 格子内原子体積占有率：74%, 例 Mg, Hf, Ru, Os, Zn, Cd
体心立方格子
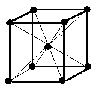面心立方格子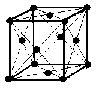
原子数…(1/8)×8 + 1 = 2 原子数…(1/8)×8 + (1/2)×6 = 4
六方最密構造
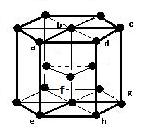
原子数…(1/6)×12 + (1/2)×2 + 3 = 6
abcdefghは：原子数…(1/8)×8 + 1 = 2
[ステップ問題2]の解答・・・(ア)(4.27 × 10-8)3(イ)7.785 × 10-23(ウ)4(エ)63.6(オ)6.02×1023
(カ)4.226×10-22(キ)2(ク)16.0(ケ)5.316 ×10-23(コ)47.58×10-23
(サ)6.11
ﾋﾝﾄ
●単位格子の体積は (4.27 × 10-8)3 cm3, 銅原子の質量は {63.6/(6.02×1023)}×4 g, 酸素原子の質量は {16.0/(6.02×1023)}×2 g
単位格子の質量は：単位格子内の銅原子の質量 + 単位格子内の酸素原子の質量
密度は：(単位格子の質量)/(単位格子の体積)
[ステップ問題3]の解答・・・(ア)積み重ね(イ)重なる(ウ)隅(エ)中心(オ)4(カ)示されていない
(キ)同等の状態
ﾋﾝﾄ
●[結晶系] 結晶格子の分類には, ﾌﾞﾗﾍﾞ格子による次のような分類がしばしば使われる。
三つの結晶軸(a, b, c)とその間の角(α,β,γ)によって次のI〜VIIの7個の系に分けられ, さらに分類すると(1)〜(14)の14個になる。
I. a≠b≠c, α≠β≠γ≠90°三斜晶系
(1)単純P (例)重ｸﾛﾑ酸ｶﾘｳﾑ
II a≠b≠c, α=γ=90°≠β(またはα=β=90°≠γ) 単斜晶系
(2)単純P, (3)底心C(またはB) (例)単斜硫黄
III.a≠b≠c, α=β=γ=90° 斜方晶系
(4)単純P, (5)底心C (6)体心I, (7)面心F (例)斜方硫黄
IV.a=b ≠c, α=β=90° γ=120°. 六方晶系
(8)単純P (例)石墨
V.a=b=c, α=β=γ≠90° 三方晶系(菱面体晶系)
(9)菱面体P (例)方解石
VI.a=b≠c, α=β=γ=90° 正方晶系
(10)単純P, (11)体心I (例)白色ｽｽﾞ
VII.a=b=c, α=β=γ=90°. 立方晶系
(12)単純P, (13)体心I, (14)面心F (例)岩塩
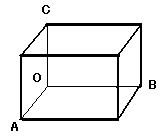
ただし, a, b, cは, OA =a, OB = b, OC =c α,β,γは, ∠BOC =α, ∠COA =β, ∠AOB =γ
P…単純格子で1個格子点(原子など)存在 F…面心の複合格子で4個格子点(原子など)存在
I…体心の複合格子で2個格子点(原子など)存在 A, B, C…bc, ca, ab面に格子点(原子など)存在(image29)
[ステップ問題4]の解答・・・(ア)体心立方(イ)4(ウ)3(エ)1.11
●ﾋﾝﾄ
三斜格子P
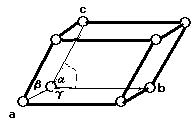単純単斜格子P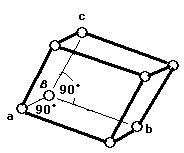
(image30) (image26)
底心単斜格子C
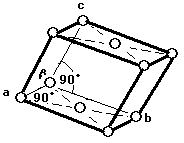体心正方格子I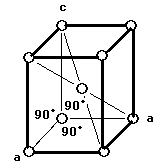 
(image27) (image28)
体心立方格子I
面心立方格子F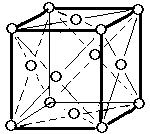 
(image22) (image24)