問1の答
理想気体の状態方程式は
pV = nRT
として表わされる。ここで p:圧力, V:体積, n:物質量, R:気体定数, および T:絶対温度。
Ansewr of Q1
The ideal gas equation is expressed as :
pV = nRT
where p:pressure, V:volume, n:amount in moles, R:gas constant, and T:absolute temperature.
問2
(i)の答 90.2 g mol-1 (有効数字3桁)
理想気体の方程式 pV = nRT を
M = (wRT)/(pV) = dRT/p
の形に書く。ここで M は見かけの分子量, w は質量, そして d は密度である。
そこで,
d = 2.74 g dm-3 = 2.74×103 g m-3,
R = 8.31 J K-1mol-1 = 8.31 Nm K-1mol-1,
T = 400 K,
そして
p = 101 kPa = 1.01×105 Pa = 1.01×105 Nm-2.
以上から
M = dRT/p = (2.74×103 g m-3)(8.31 Nm K-1mol-1)(400 K)/(1.01×105 Nm-2)
= 90.2 g mol-1
を得ることができる。
Q2
Answer of (i) 90.2 g mol-1 (3 sig. figs)
Write the ideal gas equation, pV = nRT, in the form :
M = (wRT)/(pV) = dRT/p,
where M is the apparent relative molecular mass, w is the mass, and d is the density.
So,
d = 2.74 g dm-3 = 2.74×103 g m-3,
R = 8.31 J K-1mol-1 = 8.31 Nm K-1mol-1,
T = 400 K,
and
p = 101 kPa = 1.01×105 Pa = 1.01×105 Nm-2.
From the results above, we can get
M = dRT/p = (2.74×103 g m-3)(8.31 Nm K-1mol-1)(400 K)/(1.01×105 Nm-2)
= 90.2 g mol-1
(ii)の答
エタン酸の2分子が全分子の66.7%において水素結合で結ばれているからである。いわゆるダイマーを形成することによる。
エタン酸 CH3COOH の相対式量は 2×12 + 1.0×4 + 2×16 = 60 として計算される。一方, 測定された見かけの相対分子量は (i)の答から 90.2 である。
前者と後者の質量の違いは次の理由による。エタン酸の2分子が全分子の66.7%においてともに水素結合で結ばれているからである。いわゆるダイマーを形成する。そこで, その平均分子量は (120 + 60)/2 = 90 である。
Answer of (ii)
Two molecules of ethanoic acid are associated together with the hydrogen bond in 66.7 % of the whole molecules, that is, are formed a dimer.
The relative formula mass of ethanoic acid, CH3COOH, is calculated as 2×12 + 1.0×4 + 2×16 = 60. On the other hand, the measured apparent relative molecular mass is 90.2 from the answer of (i).
There is the difference between the masses of the former and the latter because two molecules of ethanoic acid are combined together with the hydrogen bond in 66.7 % of the whole molecules, that is, form the dimer. So, the average molecular mass is (120 + 60)/2 = 90.
問3
(i)の答
 (image559)
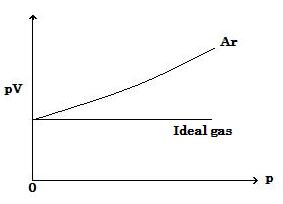
(image559)一定温度での 1 mole の理想気体の式は, pV = RT = 一定 である。この関係は圧力の全ての値に適用されうる。
Q3
Answer of (i)
 (image559)
(image559)The ideal gas equation in one mole at constant temperature is : pV = RT = constant. This relationship should apply for all values of pressure.
(ii)の答
Ar分子間で働く反発力のためで, そこでは分子の大きさが顕著になり, 理想気体と比較すると気体の体積がいくぶん増加する。
● 実在気体において次のことを注意することが重要である, すなわち, 理想気体挙動からの乖離(かいり)は高圧か低温のみで生じ, 普通ではほんのわずかである。
● 気体の運動論は分子自身は体積がゼロであることを仮定しているが, 上の図では, Ar分子自身の大きさは定温でのその圧力では分子間の距離に比較して顕著になる。
そこで, 分子の大きさはもはや無視できなくなり, 気体は理想の挙動から離れる。すなわち Ar気体は同じ条件下で理想気体よりも多くの空間を占めることになる。
結果として, p に対する pV は上の図に示されるように増加する。すなわち, pV のプロットは圧力に対して上向きの傾斜になる。
● 一般に, 実在気体分子間の引力は一定温度での適度の高い圧力で生じ, 続いて反発力は非常に高い圧力で生じる。それ故, p に対する pV のプロットは適度の高い圧力で下向きの傾斜を示し, 非常に高い圧力で上向きの傾斜を示す。
Answer of (ii)
It is due to repulsive forces operating between Ar molecules where the size of the molecules themselves becomes significant and the volume of gas increases some in comparison with ideal gas.
● It is important in real gases to note that the deviations from ideal gas behaviour only occur under conditions of high pressure or low temperature, and are usually quite small.
● Remember that the kinetic theory of gases assumes that the molecules themselves occupy zero volume, but, in the figure above, the size of Ar molecules themselves becomes significant relative to their distant apart at the pressure at constant temperature.
So, the molecular size can no longer be ignored and the gas deviates from ideal behaviour. The repulsive forces between the molecules increases the volume occupied by the gas : Ar gas takes up more space than ideal gas would under the same conditions.
As a result, the pV against p increases as shown in the figure above, that is, the plots of pV becomes the upward slopes against pressure.
● Generally, the attractive forces between real gas molecules occur at moderately high pressure at constant temperature, and the repulsive forces subsequently occur at very high pressure. Therefore, the plots of pV/RT against p show the downward slopes at moderately high pressure, and the upward slopes at very high pressure.