答　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　元の問題へ


問1の答

　この標準状態の語句は, 元素から形成される 1mol の化合物の反応に対して, 全ての物質は表示された温度と 1 bar の圧力で, 純粋の形で存在することを意味する。


　全ての化学反応は１つの関連するエンタルピー変化を持つ。ある任意の与えられた反応に対して, エンタルピー変化の値は次の3つの要因に依存している ： 含まれる物質の量, 温度, および圧力で, そこで反応が行われる。

　物質の標準状態は, 1 bar の圧力で, そして表記される温度, 一般に引用される 298 K において, 純粋形に存在する物質である。また, エンタルピー変化は特定物質のモル当りで測定される。

　例として, 25℃で気体の二酸化炭素の生成標準エンタルピー変化は, 気体の二酸化炭素が, 炭素のより不安定な形のダイアモンドではなくて最も安定な固体黒鉛および気体の酸素から形成されるとき, その標準エンタルピー変化である ：

　　C(s) + O2(g) → CO2(g)　　ΔH^Θ(298K) = -393.5 kJ mol^-1

　生成標準エンタルピー変化 ΔH^Θ(298K) は, 化合物の気体二酸化炭素がその元素から形成されるときの標準エンタルピー変化である。それは時々生成標準エンタルピー, あるいは標準生成エンタルピーと呼ばれる。

　ここで ：

　● 温度は表示されねばならない(この場合は, ΔH^Θのあとのカッコ内の 298 K),
　● 全ての物質はそれらにおいて標準状態で存在する, すなわち, 表示された温度と 1 bar の圧力で純粋の形で存在する,
　● エンタルピー変化は形成される化合物のモル当りで測定される。


Answer of Q1.

　This term standard state means that, for the reaction of 1 mol of compound formed from its elements, all substances are in their pure forms at the stated temperature and at 1 bar of pressure.


　All chemical reactions have an associated enthalpy change. For a given chemical reaction, the value of the enthalpy change depends on three factors ： the amounts of the substances involved, the temperature, and the pressure at which the reaction is carried out.

　The standard state of a substance is the substance in its pure form at 1 bar of pressure and the stated temperature, commonly quoted 298 K. Also, the enthalpy change is measured per mole of the specified substance.

　For example, the standard enthalpy change of formation of gaseous carbon dioxide at 25℃ is the standard enthalpy change when carbon dioxide gas is formed from most stable solid graphite(not diamond, which is the less stable form of carbon) and oxygen gas ：

　　C(s) + O2(g) → CO2(g)　　ΔH^Θ(298K) = -393.5 kJ mol^-1

　The standard enthalpy change of formation, ΔH^Θ(298K), is the standard enthalpy change when the compound gaseous CO2 is formed from its elements. It is sometimes called the standard enthalpy of formation or the standard formation enthalpy.

　Here ：

　● the temperature must be stated (in this case, 298 K in brackets after the ΔH^Θ symbol),
　● all substances are in their standard states, that is, in pure forms at the stated temperature and at 1 bar of pressure,
　● the enthalpy change is measured per mole of the compound formed.


問2の答　　　-145 [kJ/mol]


　反応熱Qと標準エンタルピー変化ΔH^Θの間の関係

　　Q = -ΔH^Θ

　である。
　そこで, 上に与えられた標準エンタルピー変化を使用して, 次の熱化学方程式が作られる ：

　　(1/2)N2(g) + O2(g) = NO2(g) - 34 [kJ/mol]　…(1)

　　C(s) + O2(g) = CO2(g) + 394 [kJ/mol]　…(2)

　　H2(g) + (1/2)O2(g) = H2O(g) + 242 [kJ/mol]　…(3)

　　C3H5N3O9(l) + (11/4)O2(g) = 3CO2(g) + (5/2)H2O(g) + 3NO2(g) + 1540 [kJ/mol]　…(4)

　ここで, 各熱化学方程式の中で, 負の数は吸熱反応そして正の数は発熱反応を示す。
　もし QNG がニトログリセリンでの生成反応熱を示すならば, 熱化学方程式は ：

　　3C(s) + (5/2)H2(g) + (3/2)N2(g) + (9/2)O2(g) = C3H5N3O9(l) + QNG [kJ/mol]　…(5)

　である。
　そこで最初に, (4) を (5) に導入すると,

　　3C(s) + (5/2)H2(g) + (3/2)N2(g) + (9/2)O2(g)
　　= {3CO2(g) + (5/2)H2O(g) + 3NO2(g) + 1540 - (11/4)O2(g)} + QNG

　よって,

　　3C(s) + (5/2)H2(g) + (3/2)N2(g) + (29/4)O2(g) = 3CO2(g) + (5/2)H2O(g) + 3NO2(g) + 1540 +QNG

　次に, 上式に (1)〜(3) を導入すると,

　　3C(s) + (5/2)H2(g) + (3/2)N2(g) + (29/4)O2(g)
　　= 3{C(s) + O2(g) - 394} + (5/2){H2(g) + (1/2)O2(g) - 242} + 3{(1/2)N2(g) + O2(g) + 34} +1540 + QNG

　よって

　　0 = 3×(-394) + (5/2)×(-242) + 3×34 + 1540 + QNG
　　QNG = 145 [kJ/mol]

　かくして, ニトログリセリンの生成標準エンタルピーΔH^ΘNG は

　　ΔH^ΘNG = -QNG = -145 [kJ/mol]

　熱化学方程式は

　　3C(s) + (5/2)H2(g) + (3/2)N2(g) + (9/2)O2(g) = C3H5N3O9(l) + 145 [kJ/mol]


　[別解]

　ニトログリセリン生成の化学式は ：

　　3C(s) + (5/2)H2(g) + (3/2)N2(g) + (9/2)O2(g) → C3H5N3O9(l)

　である。

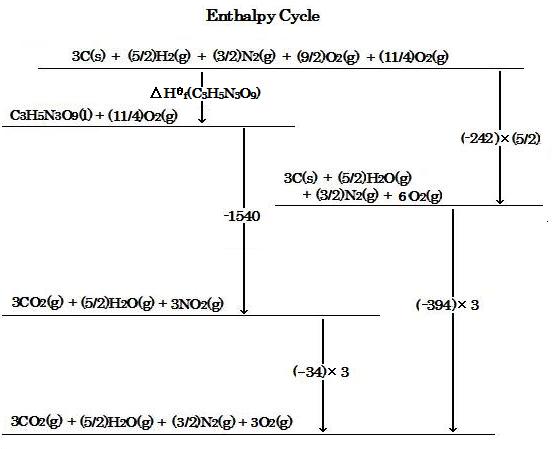
　次のエンタルピーサイクルを考慮し, ニトログリセリンの生成標準エンタルピーを計算する。その際, 上で与えられている二酸化窒素と二酸化炭素に対する生成標準エンタルピー変化, およびニトログリセリンに対する燃焼標準エンタルピー変化を使用する。
　エンタルピーサイクルの中のΔH^Θf(C3H5N3O9) と数は, 化学式に対する標準エンタルピー変化の値を示している。そこで, ヘスの法則によって, 次のように, エンタルピーサイクルから式がもたらされる ：

　　ΔH^Θf(C3H5N3O9) + (-1540) + (-34)×3 = (-242)×(5/2) + (-394)×3

　かくして,

　　ΔH^Θf(C3H5N3O9) = -145 [kJ/mol]

　　　　　.(image508)


Answer of Q2　　　-145 [kJ/mol]


　The relationship between a reaction heat, Q, and the standard enthalpy change, ΔH^Θ is ：

　　Q = -ΔH^Θ

　So, the following thermochemical equations are formed, using the standard enthalpy changes given above：

　　(1/2)N2(g) + O2(g) = NO2(g) - 34 [kJ/mol]　…(1)

　　C(s) + O2(g) = CO2(g) + 394 [kJ/mol]　…(2)

　　H2(g) + (1/2)O2(g) = H2O(g) + 242 [kJ/mol]　…(3)

　　C3H5N3O9(l) + (11/4)O2(g) = 3CO2(g) + (5/2)H2O(g) + 3NO2(g) + 1540 [kJ/mol]　…(4)

　where, in the each of thermochemical equations, the negative number represents endothermic reaction and the positive number exothermic reaction.
　If QNG shows the reaction heat of formation for nitroglycerine, the thermochemical equation is ：

　　3C(s) + (5/2)H2(g) + (3/2)N2(g) + (9/2)O2(g) = C3H5N3O9(l) + QNG [kJ/mol]　…(5)

　So first, put (4) into (5) ：

　　3C(s) + (5/2)H2(g) + (3/2)N2(g) + (9/2)O2(g)
　　= {3CO2(g) + (5/2)H2O(g) + 3NO2(g) + 1540 - (11/4)O2(g)} + QNG,

　accordingly,

　　3C(s) + (5/2)H2(g) + (3/2)N2(g) + (29/4)O2(g) = 3CO2(g) + (5/2)H2O(g) + 3NO2(g) + 1540 +QNG,

　second, put (1)〜(3) into the equation above,

　　3C(s) + (5/2)H2(g) + (3/2)N2(g) + (29/4)O2(g)
　　= 3{C(s) + O2(g) - 394} + (5/2){H2(g) + (1/2)O2(g) - 242} + 3{(1/2)N2(g) + O2(g) + 34} +1540 + QNG

　accordingly,

　　0 = 3×(-394) + (5/2)×(-242) + 3×34 + 1540 + QNG
　　QNG = 145 [kJ/mol].

　Thus, the standard enthalpy of formation for nitroglycerine, ΔH^ΘNG, is ：

　　ΔH^ΘNG = -QNG = -145 [kJ/mol],

　and the thermochemical equation is ：

　　3C(s) + (5/2)H2(g) + (3/2)N2(g) + (9/2)O2(g) = C3H5N3O9(l) + 145 [kJ/mol]


　[Another method]

　The chemical equation for the formation of nitroglycerine is ：

　　3C(s) + (5/2)H2(g) + (3/2)N2(g) + (9/2)O2(g) → C3H5N3O9(l)

　Consider the enthalpy cycle below and calculate the standard enthalpy of formation of nitroglycerine, ΔH^Θf(C3H5N3O9), using the values of the standard enthalpy changes of formation for nitrogen dioxide and carbon dioxide, and of combustion for nitroglycerine.
　So, according to Hess's law, an equation from the enthalpy cycle is brought as follows ：

　　ΔH^Θf(C3H5N3O9) + (-1540) + (-34)×3 = (-242)×(5/2) + (-394)×3

　thus,

　　ΔH^Θf(C3H5N3O9) = -145 [kJ/mol]

　　　　　


問3の答　　　-1642 [kJ/mol]


　NO2(g), CO2(g), H2O(g), および C3H5N3O9(l) に対する熱化学方程式は

　　(1/2)N2(g) + O2(g) = NO2(g) - 34 [kJ/mol]　…(1)

　　C(s) + O2(g) = CO2(g) + 394 [kJ/mol]　…(2)

　　H2(g) + (1/2)O2(g) = H2O(g) + 242 [kJ/mol]　…(3)

　　3C(s) + (5/2)H2(g) + (3/2)N2(g) + (9/2)O2(g) = C3H5N3O9(l) + 145 [kJ/mol]　…(4)

　である。
　もし QDC がニトログリセリンに対する分解の反応熱を示すならば, その熱化学方程式は

　　C3N5N3O9(l) = 3CO2(g) + (5/2)H2O(g) + (3/2)N2(g) + (1/4)O2(g) + QDC [kJ/mol]　…(5)

　である。

　そこで, (1)〜(4) を (5) に導入すると

　　{3C(s) + (5/2)H2(g) + (3/2)N2(g) + (9/2)O2(g) - 145}
　　= 3{C(s) + O2(g) - 394} + (5/2){H2(g) + (1/2)O2(g) - 242} + (3/2)N2(g) + (1/4)O2(g) + QDC

　　-145 = (-394)×3 + (-242)×(5/2) + QDC

　かくして

　　QDC = 1642 [kJ/mol],

　ニトログリセリンの分解に対するエンタルピー変化 ΔH^Θは

　　ΔH^Θ = -QDC = -1642 [kJ/mol]


　[別解]

　NO2(g), CO2(g), および C3H5N3O9(l) の生成, およびエンタルピー変化 ΔH^Θ を伴なう C3H5N3O9(l) の分解に対するエンタルピーサイクルにおいて,

　　ΔH^Θ - 145 = (-394)×3 + (-242)×(5/2),

　かくして

　　ΔH^Θ = -1642 [kJ/mol]


Answer of Q3　　　-1642 [kJ/mol]


　The thermochemical equations for NO2(g), CO2(g), H2O(g), and C3H5N3O9(l) are ：

　　(1/2)N2(g) + O2(g) = NO2(g) - 34 [kJ/mol]　…(1)

　　C(s) + O2(g) = CO2(g) + 394 [kJ/mol]　…(2)

　　H2(g) + (1/2)O2(g) = H2O(g) + 242 [kJ/mol]　…(3)

　　3C(s) + (5/2)H2(g) + (3/2)N2(g) + (9/2)O2(g) = C3H5N3O9(l) + 145 [kJ/mol]　…(4)

　If QDC shows the reaction heat of decomposition for nitroglycerine, the thermochemical equation is ：

　　C3N5N3O9(l) = 3CO2(g) + (5/2)H2O(g) + (3/2)N2(g) + (1/4)O2(g) + QDC [kJ/mol]　…(5)

　So, put (1)〜(4) into (5),

　　{3C(s) + (5/2)H2(g) + (3/2)N2(g) + (9/2)O2(g) - 145}
　　= 3{C(s) + O2(g) - 394} + (5/2){H2(g) + (1/2)O2(g) - 242} + (3/2)N2(g) + (1/4)O2(g) + QDC

　　-145 = (-394)×3 + (-242)×(5/2) + QDC

　Thus,

　　QDC = 1642 [kJ/mol],

　the enthalpy change, ΔH^Θ, for the decomposition of nitoroglycerine is ：

　　ΔH^Θ = -QDC = -1642 [kJ/mol]


　[Another method]

　In the enthalpy cycle for the formation of NO2(g), CO2(g), and C3H5N3O9(l), and for the decomposition of C3H5N3O9(l) with the enthalpy change, ΔH^Θ,

　　ΔH^Θ - 145 = (-394)×3 + (-242)×(5/2),

　thus,

　　ΔH^Θ = -1642 [kJ/mol]


問4の答

　[理由]　ニトログリセリンの分解反応がその燃焼反応よりもより発熱的であり, それ故, 前者中の反応物としてのニトログリセリンが, 発熱反応で生じた熱エネルギーを使用して, 生成物を形成すべき活性状態へより多く促進される。


　酸素を伴なうニトログリセリンの燃焼での反応は

　　C3H5N3O9(l) + (11/4)O2(g) → 3CO2(g) + (5/2)H2O(g) + 3NO2(g)　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　ΔH^Θ(combustion) = -1540 [kJ/mol]

　である。一方, 衝撃によるニトログリセリンの分解に対しては

　　C3N5N3O9(l) → 3CO2(g) + (5/2)H2O(g) + (3/2)N2(g) + (1/4)O2(g)
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　ΔH^Θ(decomposition) = -1642 [kJ/mol].

　上に与えられている式中のΔH^Θ(combustion) とΔH^Θ(decomposition) を比較すると,

　　ΔH^Θ(combustion) > ΔH^Θ(decomposition)

　これは以下のことを意味する ： ニトログリセリンの分解反応がその燃焼反応よりもより発熱的であり, それ故, 前者中の反応物としてのニトログリセリンが, 発熱反応で生じた熱エネルギーを使用して, 生成物を形成すべき活性状態へより多く促進される。
　かくして, ニトログリセリンの分解反応が燃焼反応よりもむしろ起きる。


Answer of Q4.

　The decomposition reaction of nitroglycerine is more exothermic than the combustion reaction, and therefore nitroglycerine as reactants in the former are accelerated more greatly into the activation state to form the products, using the heat energy produced with exothermic reaction.


　The reaction for the combustion of nitroglycerine with oxygen is ：

　　C3H5N3O9(l) + (11/4)O2(g) → 3CO2(g) + (5/2)H2O(g) + 3NO2(g)　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　ΔH^Θ(combustion) = -1540 [kJ/mol].

　On the other hand, for the decomposition of nitroglycerine on impact is ：

　　C3N5N3O9(l) → 3CO2(g) + (5/2)H2O(g) + (3/2)N2(g) + (1/4)O2(g)
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　ΔH^Θ(decomposition) = -1642 [kJ/mol].

　Compare ΔH^Θ(combustion) with ΔH^Θ(decomposition) in the equations given above, and, as result,

　　ΔH^Θ(combustion) > ΔH^Θ(decomposition).

　This means that the decomposition reaction of nitroglycerine is more exothermic than the combustion reaction, and therefore nitroglycerine as reactants in the former are accelerated more greatly into the activation state to form the products, using the heat energy produced with exothermic reaction.
　Thus the decomposition reaction of nitroglycerine occurs rather than the combustion reaction.


問5の答　　　+44 [kJ/mol]

　[ΔH^Θ の説明]　ΔH^Θ の値は正であり, それ故 H2O(l) → H2O(g) の過程は吸熱的である。そこで, 熱が周囲から加えられる必要がある。


　水素燃焼での 2つの化学式が次のように示される ：

　　H2(g) + (1/2)O2(g) → H2O(g)　　ΔH^Θ(H2O(g)) = -242 [kJ/mol]　…(1)

　　H2(g) + (1/2)O2(g) → H2O(l)　　ΔH^Θ(H2O(l)) = -286 [kJ/mol]　…(2)

　上に与えられている 2つの式を熱化学方程式に書き換えると

　　H2(g) + (1/2)O2(g) = H2O(g) + 242 [kJ/mol]　…(1)'

　　H2(g) + (1/2)O2(g) = H2O(l) + 286 [kJ/mol]　…(2)'

　(2)' - (1)'.を計算すると

　　0 = {H2O(l) - H2O(g)} + {286 - 242}
　　0 = H2O(l) - H2O(g) + 44

　したがって

　　H2O(l) = H2O(g) - 44 [kJ/mol],

　そしてそれ故, 過程 H2O(l) → H2O(g) に対するエンタルピー変化は

　　ΔH^Θ = +44 [kJ/mol]

　である。

　ここで, ΔH^Θ の値は正であり, それ故 H2O(l) → H2O(g) の過程は吸熱的である。そこで, 熱が周囲から加えられる必要がある。


　[別解]

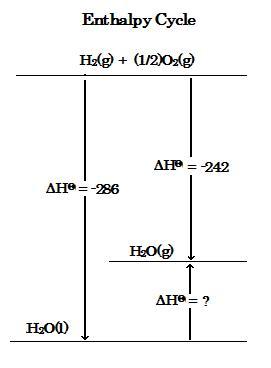
　下のエンタルピーサイクルは水生成での水素燃焼の反応に対して示されている。ΔH^Θの値はkJ/molである。
　H2O(l) → H2O(g) の過程に対するエンタルピー変化 ΔH^Θは, ヘスの法則により, 次のようにエンタルピーサイクルを使用して計算される ：

　　ΔH^Θ = (-242) - (-286) = +44 [kJ/mol]

　ここで, ΔH^Θ の値は正であり, それ故 H2O(l) → H2O(g) の過程は吸熱的である。そこで, 熱が周囲から加えられる必要がある。
　　　　　　　　　　　　　　　(image509)


Answer of Q5　　　+44 [kJ/mol]

　[Explanation of ΔH^Θ]　The value of ΔH^Θ is positive, and therefore the process H2O(l) → H2O(g) is endothermic. So heat need be added from the surroundings.


　Two chemical equations for the combustion of hydrogen are shown as follows ：

　　H2(g) + (1/2)O2(g) → H2O(g)　　ΔH^Θ(H2O(g)) = -242 [kJ/mol]　…(1)

　　H2(g) + (1/2)O2(g) → H2O(l)　　ΔH^Θ(H2O(l)) = -286 [kJ/mol]　…(2)

　Rewrite the two equations given above the thermochemical equations.

　　H2(g) + (1/2)O2(g) = H2O(g) + 242 [kJ/mol]　…(1)'

　　H2(g) + (1/2)O2(g) = H2O(l) + 286 [kJ/mol]　…(2)'

　Calculate (2)' - (1)'.

　　0 = {H2O(l) - H2O(g)} + {286 - 242}
　　0 = H2O(l) - H2O(g) + 44

　Accordingly,

　　H2O(l) = H2O(g) - 44 [kJ/mol],

　and the enthalpy change for the process H2O(l) → H2O(g), ΔH^Θ, is ：

　　ΔH^Θ = +44 [kJ/mol]

　Here, the value of ΔH^Θ is positive, and therefore the process H2O(l) → H2O(g) is endothermic. So heat need be added from the surroundings.


　[Another method]

　The enthalpy cycle below is shown for the reactions of hydrogen combustion to form water. The values of ΔH^Θ are in kJ/mol.
　The enthalpy change, ΔH^Θ, for the process H2O(l) → H2O(g), according to Hess's Law, is calculated using the enthalpy cycle as follows ：

　　ΔH^Θ = (-242) - (-286) = +44 [kJ/mol]

　Here, the value of ΔH^Θ is positive, and therefore the process H2O(l) → H2O(g) is endothermic. So heat need be added from the surroundings.

　　　　　　　　　　　　　　　　　(image509)