答　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　元の問題へ


問1の答　　α構造 ： Ag⁺,　　γ構造 ： Zn²⁺


　構造(α, γ)を持つアミン錯体を形成する金属イオンにおいて, その金属イオンは, 混成軌道を構成して, 配位子のアンミン中の窒素原子に存在する非共有電子対と配位結合する。

●　原子価結合法によって, 亜鉛イオン Zn²⁺ のアンミン錯体を考慮すると, まず亜鉛 Zn の基底状態の電子配置は,

　　Zn電子配置 ： (不活性元素Ar電子配置と同じ)3d¹⁰4s²

　そこで, Zn の周囲との相互作用によって, Zn は電子 2個を放出して, 次のような亜鉛イオン Zn²⁺ になる ：

　　Zn²⁺電子配置 ： (Ar電子配置と同じ)3d¹⁰

　さらに, Zn²⁺ は, 周囲との電気的相互作用によって, １つの4s と 3つの4p の電子軌道が 4つのγ型の sp³混成軌道を形成し,

　　γ型のZn²⁺電子配置 ： (Ar電子配置と同じ)3d¹⁰(sp³)(sp³)(sp³)(sp³)

　上述の混成軌道へアンモニア分子中の窒素原子に存在する非共有電子対を取り入れて, 4つのアンモニア分子と配位結合する ：

　　Zn²⁺ + 4NH3 → [Zn(NH3)4]²⁺

　よって, Zn²⁺ はγ型錯イオンのテトラアンミン亜鉛(II)イオンを生じる。

● Ag⁺ の場合は, Zn²⁺ と同様にして考慮すると,

　　Ag電子配置 ： (不活性元素Kr電子配置と同じ)4d¹⁰5s¹

　　Ag⁺電子配置 ： (Kr電子配置と同じ)4d¹⁰

　1つの 5s と 1つの 5p の電子軌道が 2つのα型のsp混成軌道を形成し,

　　α型の Ag⁺電子配置 ： (Kr電子配置と同じ)4d¹⁰(sp)(sp)

　そこで, 次のように, 2つのアンモニアと反応して, Ag⁺ はα型錯イオンのジアンミン銀(I)イオンを生じる ：

　　Ag⁺ + 2NH3 → [Ag(NH3)2]⁺

●　Cu²⁺ は, Zn²⁺ および Ag⁺ と同様に, 配位結合して, β型錯イオンを形成する。Na⁺ と Mg²⁺ は, 不活性元素の安定な電子配置と同じで非常に安定である。そのために, 混成軌道を生じない。したがって, Na⁺ と Mg²⁺ は, α型～δ型の錯イオンを形成しない。


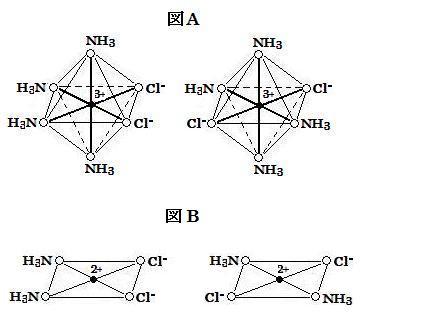
問2の答　　下図A参照　(中心の●はコバルトイオン Co³⁺ を表わす。)


　[Co(NH3)4Cl2]⁺ は八面体構造(δ)をとり, 2つの幾何異性体が存在する。そこで, 図1のδを参照して, その分子構造を描くと, 下図Aにおいて, シス形(左側)とトランス形(右側)が存在する。中心の●はコバルトイオン Co³⁺ を表わす。


問3の答　　 Fe


　ヘモグロビンは, ポリフィリン鉄錯塩とタンパク質から成るヘムタンパク質の一種で赤色を呈する。酸素や一酸化炭素などが付加する。ほ乳動物の赤血球中には 30～34%含まれる。血液中では, 9(羊)%～17(馬)%含まれる。とくに, 正常の人は14.5 % である。


問4の答　　下図B参照　(中心の●は白金イオン Pt²⁺ を表わす。)


　白金の基底電子配置は

　　Pt電子配置 ： (不活性元素Xe電子配置と同じ)5d⁹6s¹

　　Pt²⁺電子配置 ： (Xe電子配置と同じ)5d⁸

　1つの 5d, 1つの 6s および 2つの 6p の電子軌道が 4つのβ型のdsp²混成軌道を形成し,

　　β型の Pt²⁺電子配置 ： (Xe電子配置と同じ)(5d')⁸(dsp²)(dsp²)(dsp²)(dsp²)

　次のように, 2つのアンモニア分子と 2つの塩化物イオンと反応して, 幾何異性体を有する錯体を形成する ：

　　Pt²⁺ + 2NH3 + 2Cl^- → [Pt(NH3)2]Cl2

　その幾何異性体は下図Bに示されている。ただし, 中心の●は白金イオン Pt²⁺ を表わす。

　　　　　　　　　　　(image506)


問5の答　　5.0×10^-4　[mol/L]


　[問題]文中の「硬水の軟化, 水の硬度測定などは, 金属イオンと 1対 1で錯体を生成しやすい」と図2を考慮すると, Ca²⁺ と EDTA は, 次のように平衡反応で表わされ, 水素イオンを生じる ：

　　Ca²⁺ + EDTA ⇄ [Ca-EDTA] + 2H⁺　…(1)

　ここで, pH の変化は考慮しなくて良いので, この Ca-EDTA錯体の生成定数 K は

　　K = [Ca-EDTA]/([EDTA][Ca²⁺]) = 3.9×10¹⁰　[L/mol]　…(2)

　いま, Ca²⁺溶液の濃度を x [mol/L] とすると, 0.10 [L]中の Ca²⁺ の物質量 MCA は

　　MCA = 0.1x 　[mol]

　一方, (1)式において, Ca²⁺ と反応する EDTA の物質量 MED は, モル濃度が 0.010 mol/L であるので,

　　MED = 0.010×(5/1000) = 5.0×10^-5　 [mol]

　そこで, (1)の平衡で各化学種の濃度は, 容積は(0.10 + 0.005) L から

　　[Ca²⁺] = (0.1x - 5.0×10^-5)/0.105　 [mol/L]　…(3)

　　[EDTA] = [0.010 - 5.0×10^-5] = 0.00995　 [mol/L]　…(4)

　　[Ca-EDTA] = (5.0×10^-5)/0.105 ≒ 47.62×10^-5　 [mol/L]　…(5)

　(3), (4) および (5) を (2) に代入すると

　　K = [Ca-EDTA]/([EDTA][Ca²⁺]) = (47.62×10^-5)/[0.00995×{(0.1x - 5.0×10^-5)/0.105}]

　　　= 3.9×10¹⁰

　上式を変形すると,

　　(47.62×10^-5)×0.105 = (3.9×10¹⁰){0.00995×(0.1x - 5.0×10^-5)}
　　5.0001×10^-5 = 0.038805×10¹⁰(0.1x - 5.0×10^-5)
　　5.0001 = 0.038805×10¹⁵(0.1x - 5.0×10^-5)
　　128.8×10^-15 = 0.1x - 5.0×10^-5
　　0.1x = 128.8×10^-15 + 5.0×10^-5 = 1.288×10^-13 + 5.0×10^-5 ≒ 5.0×10^-5

　よって,

　　x = 5.0×10^-4　[mol/L]

　[別解]

　Ca²⁺溶液の濃度を x [mol/L] とすると, Ca²⁺ と EDTA は同物質量で反応することから, 次式が成立する ：

　　(0.010)×(5.0/1000) = (x)×(0.10)

　よって,

　　x = {(0.010)×(5.0/1000)}/0.10 = 5.0×10^-4　[mol/L]


問6の答　　活性化エネルギー


　化学反応において, 反応物と生成物の間には, 一般に, エネルギーの山が存在し, 反応速度をコントロールしている。このエネルギーの山を活性化エネルギーと呼ぶ。したがって, 活性化エネルギー値が小さいと, 反応速度は大きくなる。逆に活性化エネルギーが大きいと, 反応速度は小さくなる。反応に触媒の作用があると, 触媒は, 間接的に反応速度だけに影響を与える。