[問題] 1882年頃アレニウスは, すべての電解質について, 酢酸と同様に分子状に溶解した電解質分子が部分的に電解すると考えていた。しかし, 今日では塩化カリウムなどのイオン結晶は, KClのような単位の分子状の溶解状態は存在せず, すべてがイオンとして存在していることがわかっている。
したがって, 既述類題1-1(100502)中の(1)式:α= q/(p + q) のαは1となるはずである。しかし, この類題1-1中の表1にあるように, 電気伝導度の測定から得られたαは1より小さい。その理由について既述類題1-1を参照しながら以降で考察する。
以下の各問いに答えなさい。答に至る過程も示すこと。必要であれば次の各元素の原子量を用いなさい。H=1.0, C=12.0, N=14.0, O=16.0, Mg=24.3, S=32.1, Cl=35.5, K=39.1, Ca=40.1, Sr=87.6, Cd=112.4
問1. イオン結晶のKClなどの強電解質では, 水溶液中ではすべてが解離したイオンとして存在しているが, 濃度が高くなると, 陽イオンのまわりに陰イオンが, 陰イオンのまわりには陽イオンが存在しやすいために, 見かけ上, イオンの濃度が減少する。この時, 電気伝導度や浸透圧に寄与する「見かけ上のイオン濃度」を生じる強電解質の濃度を「活量」と呼ぶ。
また, 活量に関与する物質量を, 溶解した全物質量で割ったものを「活量係数」(γ)と呼ぶ。デバイとヒュッケルの理論によれば, 電解質ABの溶解でイオンAZ+とBZ- が生成するとき, 活量係数γは次式で表される。
log10γ= -0.5z3C1/2 (6)
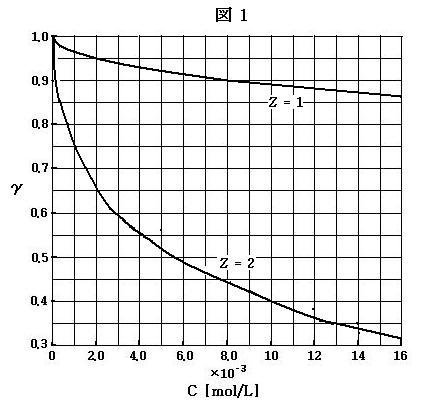
ここで, Cは溶解した電解質ABのモル濃度[mol/L]である。すなわち, CはAZ+またはBZ- の濃度であり, AZ+とBZ-の濃度濃度の和ではない。z = 1および z = 2 について, (6)式のγを Cに対してプロットしたものを下の図1に示す。
KCl などの強電解質については, アレニウスの電気伝導度測定による活動度係数αは活量係数γに等しいと考えられる。
既述類題1-1(100502)中の表1の塩化カリウムおよび硫酸マグネシウムの2つについて, 1g の物質を水に溶解して 1L とした濃度におけるγの値を下の図1を使用して求めなさい。
答
問2. アレニウスが導いた i とαの関係式, いわゆる, 既述類題1-1(100502)中の(4)式:i = 1 + (k - 1)αは, 酢酸などの電離平衡を想定したものであり, αは解離度に相当する。ここで, 強電解質の塩化カリウムなどの溶解ではαは上記の活量係数γに等しいと考えられるが, (4)式は, そのままでは成立しない。
αはγと一致する場合は, 浸透圧に寄与するイオンの活量は, 溶解した全てのイオンの濃度に活量係数γをかけることで得られる。
強電解質の塩化カリウムなどにおいて, 活量係数γから i を求める式を書きなさい。
答
問3. 既述類題1-1(100502)中の表1の塩, 特に硫酸塩では(4)式から計算された i 値(表1の最右端の列))は, 浸透圧から得られた i 値(表1の最右端から2番目の列)より大きな値を示す。これは, 上の問2で見たように, 電離平衡を想定した(4)式から i を計算していることに原因があると考えられる。
表1の塩化カリウムおよび硫酸マグネシウムの2つについて, 上の問2で導いた式から, 最右端の列の i の値を再計算しなさい。ただし, γには, 問1で求めた値を用いなさい。
答
 (image310)
(image310)