[問題] 次の文は1882年に発表されたアレニウスの電離説に関する論文の要約です。これを読んで下の各問いに答えなさい。
二年前にスウェーデン科学アカデミーに提出されたファントホッフの論文の中で, 気体に関するアボガドロの法則, すなわち「ある温度で一定の数の分子を一定体積に含む気体は, 気体の種類によらず等しい圧力を示す」が以下のように一般化されることを示した。
『ほとんどの物質について, Aある温度 T で, 一定の物質量 n の物質を任意の液体に溶解した体積 V の溶液が示す浸透圧は, 同じ温度 T で, 同じ物質量 n の分子を同じ体積 V に含む気体が示す圧力と等しい。』
しかし, この法則は, すべての物質について成立するわけではない。特に水溶液については, かなり多くのものが法則の例外であり, 法則よりも著しく大きな浸透圧を示すことがわかっている。
また, 気体にもアボガドロの法則よりも著しく大きな圧力を示す例がある。高温における塩素や臭素, ヨウ素のふるまいは, その代表例である。これらの物質は, 高温では原子に解離しているので, 見かけ上アボガドロの法則から外れると考えられている。水溶液でファントホッフの法則の例外とされている物質についても, 同じような説明が適合されると思われる。
この論文の目的は, このような説明が水溶液の電気伝導度の測定からも強く支持されることを示すことにある。水溶液の電気伝導現象は『電解質分子(*訳注1)の一部は, 互いに独立に動くことのできる「イオン」に解離している』という仮説に基づいて説明される。したがって, どれだけの割合の電解質分子がイオンに解離しているかがわかれば, ファントホッフの法則から浸透圧を計算することが可能となることになる。
私は以前に「電解質の電気伝導性に関して」と題した論文で, 互いに独立に動けるイオンに解離した分子を「活性」, 解離していない分子を「不活性」と呼んだ。そして無限希釈においてすべての電解質分子は活性になると考えられることを示した。
以下の計算もこの仮説に基づいている。活性な分子の数をq, 不活性な分子数をpとしたとき, 活性な分子の割合, 「活性度係数」(α)は以下のようになる。
α= q/(p + q) (1)
このαは無限希釈において 1 になるはずである。電解質分子の濃度が高い場合αは 1 より小さくなるが, 以前の論文に示したように, 水溶液の電気伝導度の測定からαを導くことができる。
一方, ファントホッフは, 実際の浸透圧(Π)を, 物質がすべて不活性であると仮定して計算される浸透圧(Π0)で割ったものを係数 i として報告している。
i = Π/Π0 (2)
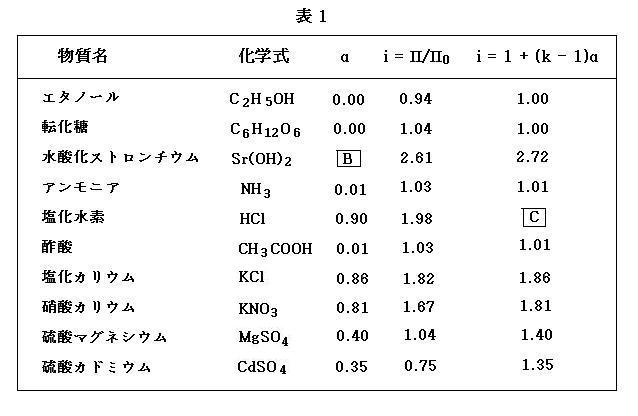
この値を次の表1(image308)の右から2番目の列に示した(*訳注2)。そこで, 電解質分子が解離した結果生じるイオンの一つ一つが, 一つの分子として浸透圧に寄与するとすれば次式が得られる。
i = (p + kq)/(p + q) (3)
ここで k は一つの活性分子が解離して生成するイオンの数(たとえば KCl について k = 2, すなわち K+ + Cl- であり, BaCl2 あるいはK2SO4 については, k = 3, つまり Ba2+ + 2Cl-, あるいは 2K+ + SO42- )である。
さて, (1)式と(3)式から, 以下のように i をαを用いて表すと次のようになる。
i = 1 + (k - 1)α (4)
αは電気伝導度の測定から求めることができるので, k を仮定すれば, 電気伝導度の測定からも i が求められる。表1の活性係数αは 1g の物質を水に溶かして 1 L(㍑)にした濃度における値であり, 表1の右端の列には, このαを用いて(4)式から計算された i を示してある。
表1の右端の2つの列の数値, すなわち, 浸透圧から求めた i と, 電気伝導度の測定から(4)式を用いて計算された i には特筆すべき一致が見られる。このことは(4)式を導く際に用いた以下の仮定が正しいものであることを示している。
1) 水溶液中の電解質分子には, 陽イオンと陰イオンに解離した活性な分子と, 解離しないまま存在する不活性な分子がある。解離によって生成したイオンの数も, ファントホッフの浸透圧の法則の分子数として寄与する。
2) 不活性な分子は, 溶液を希釈していくにつれ活性にかわる。無限希釈はすべての分子が活性になる。
これら2つの仮定は理論的な意味だけでなく, 実用的な意味でも重要である。この論文では, 従来ファントホッフの法則の例外とされていた物質についても, 陽イオンと陰イオンへの解離を考えることで法則が適用できることを示してきた。このようにファントホッフの法則が一般的に適用できるなら, 我々は, 物質(液体に溶けさえすればどんな物質でも)のD分子量を決定する非常に便利な方法を手にしたことになるのである。
(*訳注1) 現在の理解とは異なるが, 当時アレニウスは, すべての電解質はいったん分子の形で水に溶解し, その一部がイオンに解離すると考えていた。文中の「電解質分子」という表現は, この分子状の溶解物を指している。
(*訳注2) 実際には, アレニウスはこの i の値として, ラウールの凝固点降下の実験結果から得られたものを用いている。
下の各問いに答えなさい。必要であれば次の数値を用いなさい。気体定数 R = 8.3Pa・m3/(K・mol) = 0.082atm・L/(K・mol), 原子量は C=12, O=16, H=1。
問1. 下線部 A の法則(ファントホッフの法則)を, モル濃度 C から浸透圧Πを計算する形の式で書きなさい。ただし, 絶対温度を T, 気体定数を R とする。
答
問2. 下線部 D の方法は現在も分子量の測定に用いられている。ファントホッフの示した測定値によれば, 温度12℃において, ショ糖の1.2%(重量パーセント)水溶液の示す浸透圧は8.3×104 Pa(0.82atm)であった。この測定値からショ糖の分子量を求めなさい。水溶液の密度は1.0 g/cm3であるとする。答に至る計算過程も示すこと。
答
問3. 表1の空欄 B および C にあてはまる数値をそれぞれ求めなさい。
答
問4. 表1のエタノールから硝酸カリウムまでの8つの物質のうち, この論文以前に, ファントホッフの法則から著しく外れる[例外]とされていたと考えられるもの全てにおいて物質名おとびその化学式を書きなさい。
答
問5. 酢酸は分子の形で水に溶解し, その一部が電離平衡によってイオンに解離している。この場合, アレニウスの活性度係数αは電離度に等しいと考えられる。以下の式(5)に示す CH3COOH の電離平衡定数 K を用いて, 1g の物質を水に溶解して 1 L とした濃度における電離度αを計算しなさい。計算の際, αは 1 より十分小さいと仮定しなさい。
K = [CH3COO-][H+]/[CH3COOH] = 1.5×10-5 mol/L (5)
答