[問題] 下の文章を読み, 各問に答えなさい。
ファントホッフは, 図1-1に示すような仮想的な反応箱中での気体分子の化学反応を理論的に考察し, ①気体反応の濃度平衡定数が温度のみに依存することを示した。
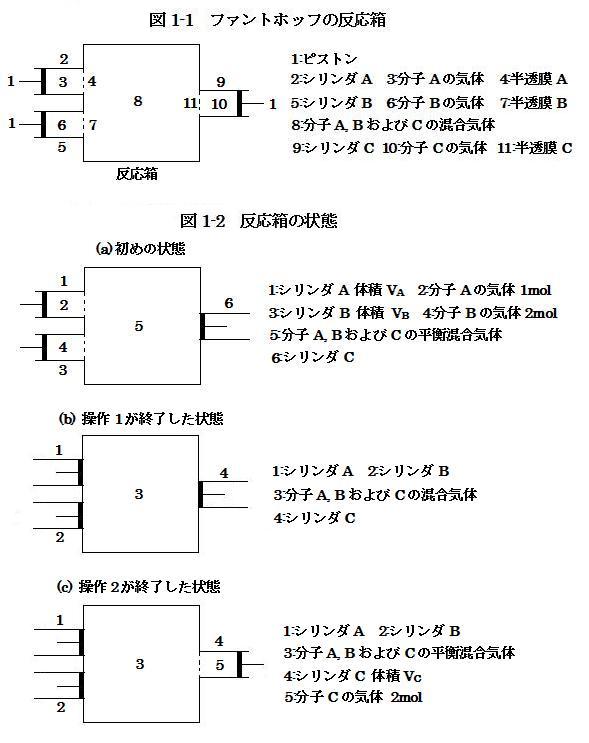(image518)ファントホッフの考察に関連して, 以下に(1)式で表される気体分子の反応を例として, 反応箱への気体分子の出し入れ操作を説明する。ここで, A, B および C は3種類の異なる分子の化学式を表わす。ただし, 反応(1)は反応箱でのみ進行するものとする。また, 気体は理想気体とみなせるものとする。
A + 2B ⇄ 2C (1)
反応箱中には気体A, B および C の混合気体が含まれており, 反応箱とシリンダは一定温度T[K]に保たれている。反応箱に装備されている半透膜Aは分子Aのみを通し, 半透膜の両側(シリンダ側と反応箱)における分子Aの示す分圧が等しくなると, 見かけ上, 半透膜Aを通る分子Aの移動はなくなる。ここで, 半透膜Aの両側における分子Aの分圧の差は速やかに解消されるものとする。半透膜B, Cの分子B, 分子Cに対する動作もそれぞれ同様であるとする。
以下に示すような手順によって, 左側の2つのシリンダA およびB 内の気体を反応箱に導入し, 反応箱から右側のシリンダC 内へ気体を移すことを考える(図1-2)。
準備 図1-2(a)に示された状態の初めの状態とする。すなわち, シリンダA および B 内にはそれぞれ 1 mol の分子A と 2 mol の分子B が含まれており, シリンダ C の体積はゼロである。このとき, シリンダA および B 内にある分子と反応箱中にある分子はそれぞれ半透膜の両側で同じ分子を示しており, 反応箱中では(1)式で表される反応は平衡状態となっている。②ここで, シリンダA, B の体積はそれぞれ VA, VB [L]であり, 濃度平衡定数は K であった。
操作1 左側の2つのピストンを押し込んで, シリンダA および B 内の気体を全て反応箱に移動させる(図1-2(b))。なお, 反応箱中での反応は十分に遅く, この操作の直後では, 反応箱中の混合気体は平衡状態にはないものとする。
操作2 反応箱中の混合気体が平衡状態となるのを待ってから, 右側のピストンを引き出してシリンダC内に 2 mol の分子Cを取り込む(図1-2(c))。この間, ピストンは非常にゆっくりと動かされており, シリンダの体積が変化しているにもかかわらず, 反応箱中の混合気体は平衡状態に保たれているとする。
問1 下線部①に関連して, 化学反応が化学平衡の状態にあるとき, 反応物質の濃度と生成物質の濃度との間には, 温度が一定ならば数量関係がある。この法則名を記しなさい。
答
問2 操作1の終了後, 十分長い時間が経過すると反応箱中の混合気体は平衡状態になる。(1)式で表される反応はどちら向きに進行しましたか。判断理由となる原理の名称とともに50字から100字程度で記しなさい。
答
問3 操作2が終了したとき, 反応箱中の混合気体は平衡状態となっている。反応箱中の混合気体の平衡は, 初めの状態と操作2の後ではどのような関係にありますか。下記の選択肢(i)～(iii)の中から適切なものを選びなさい。また, それが適切であると考えた理由を50字から100字程度で記しなさい。
図1-2(a)と比べると, 図1-2(c)における平衡混合気体では, 式(1)において,
(i) 平衡が左に移動している。 (ii) 平衡がどちら側にも移動していない。 (iii) 平衡が右に移動している。
答
問4 下線部②で与えられているシリンダの体積 VA, VB および濃度平衡定数 K を使って, 操作2が終了したときのシリンダCの体積 VC を表わしなさい。答に至る計算過程も記しなさい。
答
問5 (1)式で表される反応が反応箱中で平衡状態に達した後, 温度を上昇させると反応は左向きに進行して新たな平衡状態に達した。右向きの反応を正反応とするとき, 正反応は吸熱反応ですか発熱反応ですか。50字以内の理由とともに記しなさい。
答