問1の答 ア ： F
水素とハロゲンの結合において, 表1中のデータを用いて, ΔE の値を求めると
HF において,
ΔEH-F = E(H-F) - (1/2){E(H-H) + E(F-F)] = 5.7×102 - (1/2){4.3×102 + 1.5×102}
= 2.8×102 kJ/mol
HCl において,
ΔEH-Cl = E(H-Cl) - (1/2){E(H-H) + E(Cl-Cl)] = 4.3×102 - (1/2){4.3×102 + 2.4×102}
= 0.95×102 kJ/mol
HBr において,
ΔEH-Br = E(H-Br) - (1/2){E(H-H) + E(Br-Br)] = 3.6×102 - (1/2){4.3×102 + 1.9×102}
= 0.5×102 kJ/mol
HI において,
ΔEH-I = E(H-I) - (1/2){E(H-H) + E(I-I)] = 2.9×102 - (1/2){4.3×102 + 1.5×102} = 0 kJ/mol
以上の計算結果から, 水素元素に対する各ハロゲン元素の電気陰性度の差の絶対値 ΔE において, その大きさの順序は
ΔEH-F > ΔEH-Cl > ΔEH-Br > ΔEH-I
よって,
水素原子とハロゲン原子の間の電子を引きつける能力を表わす電気陰性度において, その電気陰性度の最も大きいハロゲン元素は, フッ素 F であることがわかる。
問2の答
{イ ： ②} {ウ ： ①} {エ ： ①} {オ ： ②} {カ ： ①} {キ ： ①}
● 原子 X の第一イオン化エネルギーは, その原子が電子を失って, イオンに変る反応の際に加えられる必要なエネルギー E である。
X(g) + E(加エネルギー) → X+(g) + e-
● 原子 X の電子親和力は, その原子が電子を得て, イオンに変る反応の際に放出されるエネルギー E' である。
X(g) + e- → X-(g) + E'(放出エネルギー)
● 原子 X の電気陰性度は, イオン化エネルギーが大きく, 電子親和力が大きい元素ほど大きくなる傾向がある。
問3の答
I ： 2.8×102 II ： 0.39 III ： 1.7
● H原子に対するF原子結合の電気陰性度の差の絶対値 ΔEは, 問1の解説を参照して, 次のようになる.
ΔEH-F = E(H-F) - (1/2){E(H-H) + E(F-F)] = 5.7×102 - (1/2){4.3×102 + 1.5×102}
= 2.8×102 kJ/mol
● 結晶において, 体心立方格子, 面心立方格子および立方最密構造は次のように示される。また, 結晶の配位数は注目球状粒子を取り巻く最も近い他の粒子の数を意味する。
(1)体心立方格子(image1)・・・配位数：8, 格子内粒子数：2, 格子内粒子体積占有率：68%
(2)面心立方格子(image2)・・・配位数：12, 格子内粒子数：4, 格子内粒子体積占有率：74%
(3)六方最密構造(image6)・・・配位数：12, 格子内粒子数：6, 格子内粒子体積占有率：74%
体心立方格子
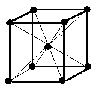面心立方格子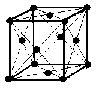
粒子数…(1/8)×8 + 1 = 2 粒子数…(1/8)×8 + (1/2)×6 = 4
配位数：8 配位数：12
六方最密構造
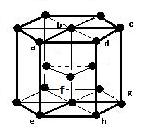
粒子数…(1/6)×12 + (1/2)×2 + 3 = 6
abcdefghは：原子数…(1/8)×8 + 1 = 2
配位数：12
● CO2の分子結晶において, その分子が面心立方格子を形成し, 直線形CO2分子の真ん中にあるC原子中心が立方格子の頂点と面心を占めている。
この結晶において, 1つのCO2分子に含まれるC原子から最も近い位置に存在するC原子は, 上図の面心立方格子を参照して, 立方格子面の対角線上に存在する。そこで, その対角線上において, 1つのC原子中心から最も近い位置のC原子中心までの距離を X [nm] とすると, ピュタゴラスの定理を用いて, 次式が成立する。
(2X)2 = (0.56)2 + (0.56)2
4X2 = 0.6272
よって,
X = (0.1568)1/2 = (1568/10000)1/2 = (1/100)×(16×2×49)1/2
= 0.01×4×21/2×7 = 0.28×21/2 = 0.28×1.4 = 0.39 [nm]
● 立方格子内に存在するCO2分子は, 上述の面心立方格子図を参照して, CO2の分子は立方格子内に4個存在していることになる。したがって, 立方格子の質量 M [g] は, CO2の分子量は 12.0 + 16.0×2 = 44.0 であるので,
M = {44.0/(6.0×1023)}×4 = 29.3×10-23 [g]
一方, 立方格子の体積 V [cm3] は
V = (0.56×10-7)3 = 0.176×10-21 = 17.6×10-23 [cm3]
よって, 立方格子の密度 d [g/cm3] は
d = M/V = (29.3×10-23)/(17.6×10-23) = 29.3/17.6 = 1.7 [g/cm3]
問4の答
水は二等辺三角形の分子である。そこで, O と H の電気陰性度の差によって O-H で電気モーメントが生じ, H-O-H の電気モーメントのベクトル和はゼロにならい。したがって, 分子内で電荷のかたよりが生じ, 水は極性分子となる。一方, 二酸化炭素は, 直線形の分子であるので, O=C=O の電気モーメントのベクトル和はゼロとなり, 無極性分子となる。