[問題] 次の文を読んで, ( ア )〜( カ )に適した式を記入しなさい。
シリカゲルや活性炭などの物質は多孔質物質と呼ばれる。多孔質物質は広い表面積を持つことが知られており, その表面に多くの気体分子が付着する。この現象を吸着といい, 多孔質物質は乾燥剤や脱臭剤として利用されている。
以下では吸着現象の原理について考え, 多孔質物質の表面積を実験的に求める方法を考えてみよう。多孔質物質の表面には気体分子を吸着できる場所(以下, 吸着点と呼ぶ)が存在する。その総数を N0 とし, そのうちN個の吸着点が気体分子を吸着しているものとする。
各吸着点は気体分子を 1個しか吸着できないものとする。また吸着された気体分子の間に相互作用はなく, 化学反応も起らないものと仮定する。
単位時間あたりに多孔質物質が吸着する気体分子の数 ra は, 気体の圧力 P と空いている吸着点の数に比例する。このとき比例定数 ka を用いると, 次式のように表わされる。
ra = kaP×( ア ) …(1)
一方, 吸着された気体分子の脱離も起る。単位時間あたりに脱離する気体分子の数 rd は気体分子を吸着している吸着点の数, つまり吸着された気体分子の数に比例する。このとき比例定数 kd を用いると, 次式のように表わされる。
rd = kd×( イ ) …(2)
気体と多孔質物質を接触させると, 一定量の気体分子が吸着され平衡状態となる。このとき, 単位時間あたり, 多孔質物質表面に吸着する気体分子の数は, 吸着点から脱離する気体分子の数に等しい。ここで ka/kd を K とおくと, N は N0, K, P を用いて次式のように表わされる。
N = ( ウ ) …(3)
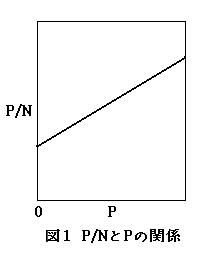
(3)式について, P/N を P の関数と考えると図1のような直線関係が得られる。その傾きは( エ )と表され, P/N 軸の切片は( オ )となる。したがって 2つの異なる平衡状態での圧力 P1, P2 における気体分子の吸着量 N1, N2 を実験で求めることができれば, 多孔質物質の吸着点の総数 N0 は次式で表される。
N0 = (P2 - P1)/( カ ) …(4)
さらに, 吸着された気体分子 1個が多孔質物質の表面を占める面積がわかれば, 最終的に多孔質物質の表面積を見積もることができる。
答
 (image451)
(image451)