問1の答
I…2.5, II…3.0, III…5.0
(ア:V[AH]X ) (イ:0.2([AH]aq + [A-]aq) ) (ウ:8/(1 + Ka/[H+]aq) )
(エ:-(pH + logKa)) (a.大き) (b.小さ)
ヒント
● AH ⇄ A- + H+ において, 25℃で
Ka = [A-]aq[H+]aq/[AH]aq = 4.5×10-5 mol/L
ここで, 弱酸では
[A-]aq = [H+]aq, [AH]aq>[A-]aq
よって, 弱酸のモル濃度:0.20 mol/Lは,
0.20 ≒ [AH]aq
②式において,
Ka = [A-]aq[H+]aq/[AH]aq = ([H+]aq)2/0.2 = 4.5×10-5 mol/L …(a)
(a)式から,
[H+]aq = 3×10-3 mol/L
よって,
pH = -log[H+]aq = -log(3×10-3) = 3 - log3 = 3 - 0.48 ≒2.5(答I)
● 図1において
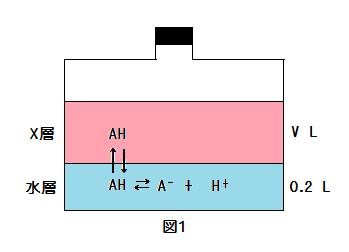
n1 = V[AH]X(答ア) n2 = 0.2([AH]aq + [A-]aq)(答イ)
n0 = n1 + n2
● 図1で, X層のV L を 0.2 Lとすると, ⑤式は
n1 = 0.2[AH]X
0.20 mol/Lの弱酸水溶液0.2 L, [AH]X/[AH]aq = 8.0 および n0 = n1 + n2 から
n0 = 0.2モル×(0.2リットル/1リットル) = 0.04 mol
n1 + n2 = V[AH]X + 0.2([AH]aq + [A-]aq) = 0.2(8[AH]aq) + 0.2[AH]aq = 1.8[AH]aq
よって,
1.8[AH]aq = 0.04
∴ [AH]aq = 0.04/1.8
したがって, Ka = [A-]aq[H+]aq/[AH]aq = 4.5×10-5, [A-]aq = [H+]aq から
([H+]aq)2/(0.04/1.8) = 4.5×10-5
よって
[H+]aq = 10-3 mol/L
pHは
pH = -log[H+]aq = -log10-3 = 3(答II)
● 図1において, ふた(黒部分)を開けて, さらに 0.10 mol/LのNaOH水溶液 0.20 Lを加えると, 水層で体積が 0.40 L になり次の中和反応が生じる。
HA + NaOH → Na+ + A- + H2O …(b)
上式で, NaOHの物質量は 0.10(mol/L)×0.20(L) = 0.02 mol になり, それと反応するHAも 0.020 molで消費される。同時にA-が0.02 mol 生じる。したがって, 水溶液 0.04 L 中に存在する未反応のHAの物質量は
未反応のHAの物質量 = (最初のHA物質量) - (消費されたHA物質量)
= 0.2(mol/L)×0.2(L) - 0.02 = 0.02 mol
未反応のHAの物質量 0.02 mol が X層と水層に分配されので, いま, X層中のHAのモル濃度を[AH]X, 水層中のHAのモル濃度を[AH]aqとすると, 次式が成立する。
0.2[AH]X + 0.4[AH]aq = 0.02 …(c)
また, 分配率において
[AH]X/[AH]aq = 8.0 …(d)
Kaにおいて
[A-]aq[H+]aq/[AH]aq = (0.02/0.4)[H+]aq/[AH]aq = 4.5×10-5 …(e)
(c)と(d)から
0.2[AH]X + 0.4[AH]aq = 0.2(8.0[AH]aq) + 0.4[AH]aq
= 1.6[AH]aq + 0.4[AH]aq = 2[AH]aq = 0.02
よって
[AH]aq = 0.01 mol/L
(e)から
(0.02/0.4)[H+]aq/[AH]aq = 0.05[H+]aq/0.01 = 4.5×10-5
よって
[H+]aq = 9.0×10-6 mol/L
pHは
pH = -log[H+]aq = -log(9.0×10-6) = 6 - 2log3 ≒ 5.0(答III)
● Pを変形
P = [AH]X/([AH]aq + [A-]aq) = 8[AH]aq/([AH]aq + [A-]aq) = 8/(1 + [A-]aq/[AH]aq)
= 8/{1 + [H+]aq/([H+]aq2/Ka)} = 8/(1 + Ka/[H+]aq)(答ウ)
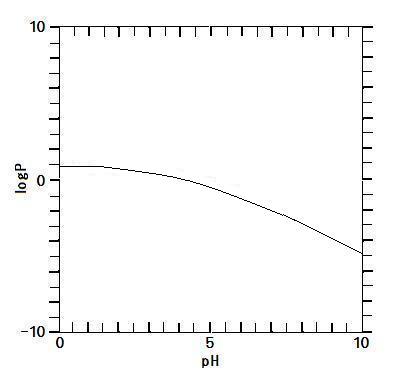
P = 8/(1 + Ka/[H+]aq)において
[H+]aq≫Kaでは
P = 8.0(一定)
よって, pH≪4.34において
(pH = -log [H+]aq≪-logKa = -log(4.5×10-5) = 5 - log(32/2) = 5 + log2 - 2log3 = 4.34)
logP = 3log2 = 0.90(一定) …(f)
[H+]aq≪Ka(pH≫4.34)では, ⑧式は
P = 8/(1 + Ka/[H+]aq) = 8/(Ka/[H+]aq)
両辺で対数を取ると
logP = -log(Ka/[H+]aq) + log8 = -(pH + logKa) + log8
= -pH + 5.24 …(g)
上の式の-(pH + logKa)は(答エ)
問2の答
 (image185)
(image185)ヒント
[H+]aq≫Ka… [H+]aq/Ka≫1 において, X/Y≧1000では (X + Y)1/2 = X1/2を考慮すると,
X = [H+]aq, Y = Ka として[H+]aq/Ka≧1000 で
([H+]aq≧4.5×10-2…log[H+]aq≧4.5×10-2…pH = -log[H+]aq≦2-log4.5 = 1.3468)
(X + Y)1/2 = ([H+]aq + Ka)1/2 = [H+]aq1/2
P = 8/(1 + Ka/[H+]aq)= 8/{([H+]aq+ Ka)/[H+]aq}= 8/([H+]aq/[H+]aq) = 8
よって, pH≦1.35において
logP = 3log2 = 0.90(一定) …(f)
[H+]aq≪Ka… Ka/[H+]aq≫1 において, X/Y≧1000では (X + Y)1/2 = X1/2を考慮すると,
X = Ka, Y = [H+]aq としてKa/[H+]aq≧1000 で
(1/[H+]aq≧1000/Ka= 2.2222×107 … pH≧7+log2.222 = 7.3468)
(X + Y)1/2 = (Ka + [H+]aq)1/2 = Ka1/2
P = 8/(1 + Ka/[H+]aq)= 8/{(Ka + [H+]aq)/[H+]aq}= 8/(Ka/[H+]aq)
両辺で対数を取ると
logP = -pH + 5.24
よって, pH≧7.35において
logP = -pH + 5.24 …(g)
問3の答
水溶液が, ある程度の酸や塩基の添加または消失があっても, ほぼ一定の水素イオン指数pHを保持するとき,その水溶液を緩衝作用があるという。一般に弱酸とその塩または弱塩基とその塩の混合水溶液が緩衝作用を示す。