答　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　元の問題へ


問1 の答

(ア.三態) (イ.引力) (ウ.変化しない) (エ.結晶 )(オ.イオン結晶 )(カ.共有結晶)
(キ.金属結晶) (ク.分子結晶) (ケ.単位格子) (コ.ﾌﾞﾗﾍﾞ)


ヒント

ﾌﾞﾗベBravais格子：7つの型(晶系)に分属する14種

I. 三斜晶系：(1)三斜格子P(単純) 　格子定数(結晶軸と軸間の角度)：a≠b≠c,  α≠β≠γ≠90°

II. 単斜晶系：(2)単純単斜格子P, (3)底心単斜格子C　格子定数：a≠b≠c,  α=γ=90°≠β

III. 斜方晶系：(4)単純斜方格子P, (5)底心斜方格子C, (6)体心斜方格子I, (7)面心斜方格子F
格子定数：a≠b≠c, α=β=γ=90°

IV. 正方晶系：(8)単純正方格子P, (9)体心正方格子I　格子定数： a=b≠c, α=β=γ=90°

V. 三方晶系(菱面晶系)：(10)菱面体格子P(単純)　格子定数： a=b=c, α=β=γ≠90°

VI. 六方晶系：(11)六方格子P(単純)　格子定数： a=b≠c, α=β=90°γ=120°

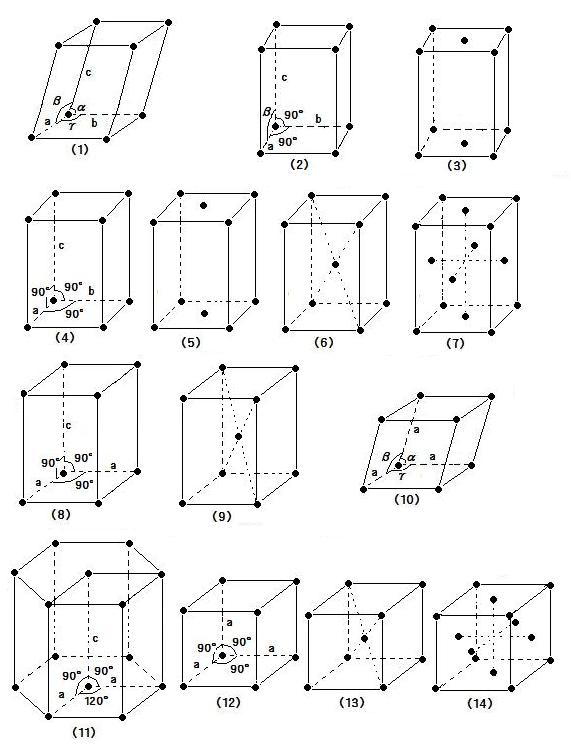
VII. 等軸晶系(立方晶系)：(12)単純立方格子P, (13)体心立方格子I, (14)面心立方格子F
格子定数： a=b=c, α=β=γ=90°

　　　　　　　　　　　　　ﾌﾞﾗベBravais格子図(image180)
　　　　　　


問2 の答

　塩化ナトリウム：NaCl, 酸化マグネシウム：MgO, ダイヤモンド：C, 石英：SiO2,
　鉄：Fe, 銅：Cu, 氷：H2O, ナフタリン：C10H8


問3 の答

面心立方格子：(d)　原子数：4　配位数：12,
体心立方格子：(b)　原子数：2　配位数： 8,
六方最密構造：(g)　原子数：6　配位数：12


ヒント

面心立方格子：(d)　原子数：(1/8)×8 + (1/2)×6 = 4　(充填率74%)
　　　　　　　　　　配位数：12…1個の原子は12個の原子と等距離で隣接している。
体心立方格子：(b)　原子数：(1/8)×8 + 1 = 2　(充填率68%)
　　　　　　　　　　配位数： 8…1個の原子は8個の原子と等距離で隣接している。
六方最密構造：(g)　原子数：(1/6)×12 + (1/2)×2 + 3 = 6　(充填率74%)
　　　　　　　　　　配位数：12…1個の原子は12個の原子と等距離で隣接している。


問4


　(1)の答　　　(A…Mg²⁺O^2-)


　(2)の答　　　(B.4) (C.22.8) (D.6.38 ) (E.6.38 ) (F.0 ) (G.7.37)


ヒント

●図1の平面abcの角の1個のNa⁺は単位格子内に(1/8)個だけ入っている。単位格子全体の8つの角では　(1/8)×8 = 1個, また, 面心の1個のNa⁺は単位格子内に(1/2)個だけ入っている。単位格子全体の6つの面では　(1/2)×6 = 3個　よって Na⁺は単位格子あたり 1 + 3 = 4個(B答)

●図1の1つの実線のCl^-は単位格子内に(1/4)個だけ入っている。単位格子全体の12辺では(1/4)×12 = 3個, また, 単位格子の体心に1個 よって Cl^-は単位格子あたり 3 + 1 = 4個(B答)

●1nm³あたりのNa⁺とCl^-のイオン数をそれぞれxとすると, 次の比例式が成立する。
　　　　　　　　　　　　　　　　(0.56)³：1 = 4：x
よって　　　　　　　　　　　　　　x = 22.8個(C答)

●平面abcに注目し, (0.56)²/2 nm²あたり, 平面abcに中心を持つNa⁺の数は{1/4 + (1/8)×2 + 1/2}=1個存在するから, 1nm²あたりの数をxとすると次の比例式が成立する。
　　　　　　　　　　　　　　　　{(0.56)²/2}：1 = 1：x
よって　　　　　　　　　　　　　　x = 6.38個(D答)
同様にして, 平面abcに中心を持つCl^-の数は(1/2)×2 = 1個存在するから, 1nm²あたりの数をxとすると次の比例式が成立する。
　　　　　　　　　　　　　　　　{(0.56)²/2}：1 = 1：x
よって　　　　　　　　　　　　　　x = 6.38個(E答)

●平面abdに注目し, {(0.56×1.414)/2}²×1.732 = 0.2715 nm²あたり, 平面abdに中心を持つNa⁺の数はゼロ個, Cl^-の数は(1/6)×3 + (1/2)×3 = 2個存在するから, 1nm²あたりの数をxとすると次の比例式が成立する。
Na⁺の数の場合：　　　　　　　　　　　x = 0個(F答)
Cl^-の数の場合： 　　　　　　　　　0.2715：1 = 2：x
よって　　　　　　　　　　　　　　　x = 7.37個(G答)


　(3)の答

[理由] 平面abcに沿って辺acの直角方向から衝撃が加えられ平面abcがずれる場合は, 必ず隣接の同イオンが近づき静電的反発による割れを起こしやすい。一方, 平面abdでのずれは隣接の同イオンの静電的反発はなく陰陽のイオンによる正負の引力で割れを起こしにくい。