[問題] 次文を読んでから下の各問いに答えなさい。
結晶は原子, イオン, 分子などの粒子が空間的周期性を持って規則的に立体的網目構造で配列している固体である。結晶の種類は, 構成する粒子の間の結合の種類に注目すると, イオン結晶, 共有結晶, 金属結晶, 分子結晶に分けられる。立体的網目構造を意味する空間格子に注目すると, 最小単位の立体の形状と対称性によって7つの型(晶系)に分属する14種の単位格子に分けられる。
格子点(粒子に相当)の配列の繰り返しを最小単位とする単位格子には, 一般にブラベBravais格子がよく使われる。同一金属原子の金属結晶は,ブラベBravais格子中の面心立方格子と体心立方格子および六方最密構造の3つから成り立つ。
問1 次の物質は, イオン結晶, 共有結晶, 金属結晶, 分子結晶の4つの結晶の中のどれに属しますか。化学式を書いて答えなさい。
氷, 石英, 酸化マグネシウム, ダイヤモンド, 鉄, ナフタレン, 塩化ナトリウム, アルミニウム
答
問2 ブラベBravais格子の7つの型(晶系)は, 格子定数(結晶軸a,b,c と軸間の角度α,β,γ)の観点から分類すると次の(A)〜(G)のようになる。下図(image180)の(1)〜(14)の各単位格子は(A)〜(G)のどれに属しますか。
(A) a=b≠c, α=β=γ=90° (B) a=b=c, α=β=γ=90° (C) a=b≠c, α=β=90°γ=120°
(D)a≠b≠c, α≠β≠γ≠90° (E)a=b=c, α=β=γ≠90° (F)a≠b≠c, α=β=γ=90°
(G)a≠b≠c, α=γ=90°≠β
答
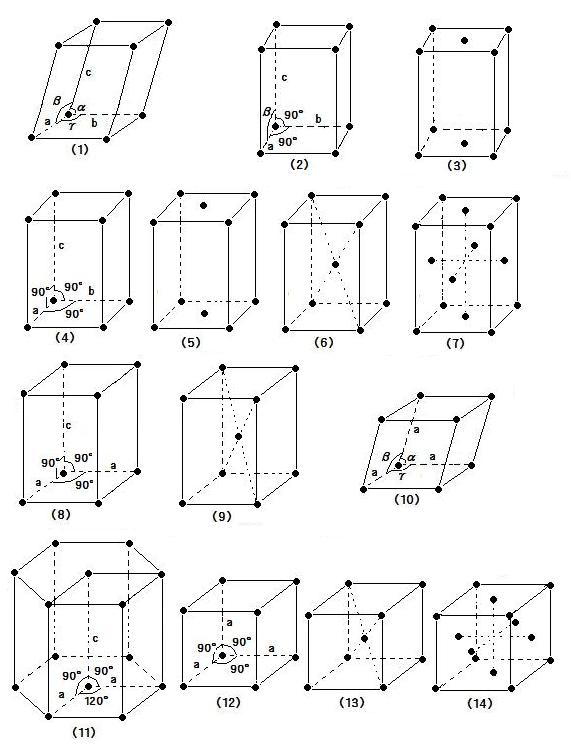
問3. (1)〜(14)の各単位格子の名称は下に掲げてある。(1)〜(14)に相当する名称を書きなさい。ただし, Pは単純, Iは体心, Fは面心, Cは底心を意味する。
[名称] 立方格子P, 正方格子P, 斜方格子I, 三斜格子P, 立方格子F, 単斜格子P, 斜方格子C, 単斜格子C, 立方格子I, 菱面体格子P, 斜方格子F, 六方格子P, 正方格子I, 斜方格子P
答
問4. (1)〜(14)の各単位格子を名称によって次の7つの型(晶系)に分けなさい。
I. 三斜晶系…
II. 単斜晶系…
III. 斜方晶系…
IV. 正方晶系…
V. 三方晶系(菱面晶系)…
VI. 六方晶系…
VII. 立方晶系(等軸晶系)…
答
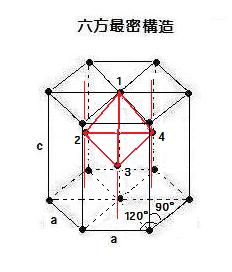
問5. 酸化アルミニウムAl2O3結晶の六方最密構造は, 酸素原子だけに注目すると, 次図のようになる。 アルミニウム原子はその格子の隙間に存在する。以下の問いに答えなさい。
 (image242)
(image242)(a) 上図のAl2O3結晶中の酸素原子だけに注目した六方最密構造において, 酸素原子1, 2, 3, 4 はブラベBravais格子(11)の中でどのような構造で配置されていますか。
答
(b) Al2O3結晶の六方最密構造中に何個の酸素原子がありますか。また, 1個の酸素原子に最近接している酸素原子は何個ですか。
答
(c) Al2O3結晶の六方最密構造には何個のアルミニウムの原子がありますか。
答
(d) Al2O3結晶の密度[g/cm3]を求めなさい。ただし, 図中のaは2.70×10-8 [cm], 答は有効数字2桁, 原子量はO:16.0, Al:27.0, アボガドロ数は6.0×1023とする。
答