[問題] 次の文章を読んで問1〜問5に答えなさい。[注意] 計算のために必要であれば, 次の値を用いなさい。原子量 : H 1.00, C 12.0, N 14.0, O 16.0 気体定数 : 8.31×103 Pa/(K・mol) 絶対零度 : -273℃.
理想気体 1 mol の温度が T (K) で, 圧力が P (Pa), 体積が V (L), 気体定数が R であるとき,
( A ) = RT …(1)
が成り立つ。式(1)では, 分子自身には大きさが無く, 分子間に引力が働かないと仮定されている。しかしながら, 実在する気体では, この仮定は成り立たない。これに対して, ファンデルワールスは分子自身の体積と分子間に働く引力を考慮して式(1)を補正し, 実在気体によくあてはまる状態方程式を導き出した。
今, 1 mol の実在気体について考えてみる。実在気体の体積 Vr は, その分子自身の体積の影響を考慮し, 分子自身の体積の効果を表わす正の定数 b を用いることで, V = ( ア ) と表わすことができる。
また, 実在気体 1 mol について体積が小さくなるほど, 分子間に働く引力は( B )になる。この分子間に働く引力により, 実在気体の圧力 Pr は理想気体の圧力に比べて( C )になるため, 分子間に働く引力効果を表わす正の定数 a を用いることで, Pr は P = ( イ ) と表わすことができる。
以上より, 1 mol あたりの実在気体について Pr, Vr, a, b を用いることで,
( D ) = RT …(2)
が導き出される。この式(2)はファンデルワールスの状態方程式とよばれ, a, b はファンデルワールスの定数とよばれている。
理想気体 1 mol では, 式(1)の右辺と左辺との比は, 常に 1 になる。この比は圧縮因子とよばれ, Z で表わす。
Z = ( A )/RT = 1
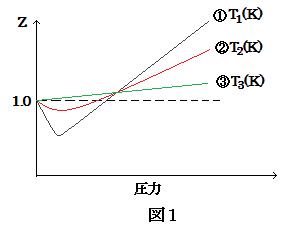
しかし, 実在気体については, 式(1)の仮定が成り立たないため, Z は 1 からずれることが知られている。図1は, ある実在気体の温度 T1(K) および T2(K), T3(K) における, 圧力と Z との関係を表わしたグラフである。ただし, 図1の温度および圧力範囲では気体状態であることは確認されている。
 (image541)
(image541)問1 空欄( ア ), ( イ ) にあてはまる式を以下の (a)〜(j) の中から選び, 記号で答えなさい。
(a) Vr + b (b) Vr - b (c) Vr×b (d) Vr÷b (e) b÷Vr (f) Pr + a/Vr2 (g) Pr - a/Vr2 (h) Pr×aVr2
(i) Pr + aVr2 (j) Pr - aVr2
答
問2 空欄( A )〜( D ) にあてはまる最も適切な語句または式を記入しなさい。
答
問3 図1より, 曲線①〜③は圧力が高いところで Z = 1 からずれ, そのずれの程度は温度により異なる。このときの温度 T1(K), T2(K), T3(K) の関係を表わす最も適切なものを以下の (a)〜(f) の中から選び, 記号で答えなさい。
(a) T1<T2<T3 (b) T1>T2>T3 (c) T2<T3<T1 (d) T2>T3>T1 (e) T3<T1<T2 (b) T3>T1>T2
答
問4 問3の解答の理由について, 以下の3つの語句をすべて使用して, 40字以内で説明しなさい。ただし, 句読点も字数に含める。
分子間力 熱運動 高温
答
問5 ある実在気体 1 mol, 27℃, 1 L におけるファンデルワールスの定数 a と b の値が, それぞれ a = 1.41×105 (Pa・L2)/mol2, b = 3.91×10-2 L/mol のとき, この実在気体の圧力を式(2)を用いて, 有効数字3桁で答えなさい。
答