問1の答 (ア.少ない)(イ.自由)(ウ.金属)(エ.結晶)
ﾋﾝﾄ
● 物質中の結合は次のように分類される。
化学結合
(1) ｲｵﾝ結合
○ 陽ｲｵﾝと陰ｲｵﾝとの間に静電的な引力(ｸｰﾛﾝ力)が働いて結合する。
(例) 塩化ﾅﾄﾘｳﾑNaCl, 硫酸ｱﾙﾐﾆｳﾑAl2(SO4)3…Al3+, SO42-がｲｵﾝ結合, 酸化ﾏｸﾞﾈｼｳﾑMgOな
ど
(2) 共有結合
○ 原子どうしが局在化した電子を共有して結合する…この結合を一般に共有結合という。
(例) 分子中の各原子の結合…ﾒﾀﾝ分子CH4のCとH, 水H2OのHとO, 塩素Cl2のClどうし
ﾀﾞｲﾔﾓﾝﾄﾞCのCどうしなど
ただし, (1)と(2)の結合をある割合で同時に含む場合が多い…極性分子
○ 原子の陽ｲｵﾝどうしが自由電子を共有して結合する…この結合を金属結合という。
(例) 銅Cuや鉄Feなどの金属
分子の間の結合
(1) 分子間力による結合
○ 分子間に作用する弱い引力でﾌｧﾝﾃﾞﾙﾜｰﾙｽ力という。一般に, 分子量の大きい分子ほど強い。さらに分子の極性による力が加わる場合がある。
(例) ﾒﾀﾝCH4分子, 酸素O2, 塩素Cl2, CO2など
(2) 水素結合
○ 分子中でﾌｯ素原子F, 酸素原子O, 窒素原子Nなどに水素原子Hが結合していると, Hを通して分子間にかなり強い結合を生じる。この結合を特に水素結合という。
(例) 水H2O, ﾌｯ化水素HF, ｱﾝﾓﾆｱNH3など
● 単体の金属結晶は, 主として次の三つの構造がある。また, 結晶の配位数は注目原子を取り巻く最も近い他の原子の数を意味する。
(1)体心立方格子(image1)・・・配位数：8, 格子内原子数：2, 格子内原子体積占有率：68%, 例 K, Ba, Ra, V, Nb, Ta, W
(2)面心立方格子(image2)・・・配位数：12, 格子内原子数：4, 格子内原子体積占有率：74%, 例 Al, Pd, Pt, Cu, Ag, Au, Pb
(3)六方最密構造(image6)・・・配位数：12, 格子内原子数：6, 格子内原子体積占有率：74%, 例 Mg, Hf, Ru, Os, Zn, Cd
体心立方格子
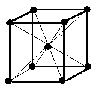面心立方格子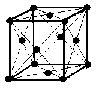
原子数…(1/8)×8 + 1 = 2 原子数…(1/8)×8 + (1/2)×6 = 4
配位数：8 配位数：12
六方最密構造
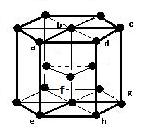
原子数…(1/6)×12 + (1/2)×2 + 3 = 6
abcdefghは：原子数…(1/8)×8 + 1 = 2
配位数：12
●[結晶系] 結晶格子の分類には, ﾌﾞﾗﾍﾞ格子による次のような分類がしばしば使われる。
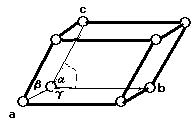
三つの結晶軸(a, b, c)とその間の角(α,β,γ)によって次のI〜VIIの7個の系に分けられ, さらに分類すると(1)〜(14)の14個になる。
I. a≠b≠c, α≠β≠γ≠90°三斜晶系
(1)単純P (例)重ｸﾛﾑ酸ｶﾘｳﾑ
II a≠b≠c, α=γ=90°≠β(またはα=β=90°≠γ) 単斜晶系
(2)単純P, (3)底心C(またはB) (例)単斜硫黄
III.a≠b≠c, α=β=γ=90° 斜方晶系
(4)単純P, (5)底心C (6)体心I, (7)面心F (例)斜方硫黄
IV.a=b ≠c, α=β=90° γ=120°. 六方晶系
(8)単純P (例)石墨
V.a=b=c, α=β=γ≠90° 三方晶系(菱面体晶系)
(9)菱面体P (例)方解石
VI.a=b≠c, α=β=γ=90° 正方晶系
(10)単純P, (11)体心I (例)白色ｽｽﾞ
VII.a=b=c, α=β=γ=90°. 立方晶系
(12)単純P, (13)体心I, (14)面心F (例)岩塩
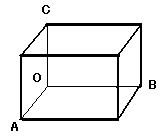
ただし, a, b, cは, OA =a, OB = b, OC =c α,β,γは, ∠BOC =α, ∠COA =β, ∠AOB =γ
P…単純格子で1個格子点(原子など)存在 F…面心の複合格子で4個格子点(原子など)存在
I…体心の複合格子で2個格子点(原子など)存在 A, B, C…bc, ca, ab面に格子点(原子など)存在(image29)
図のいくつかの具体例
三斜格子P
単純単斜格子P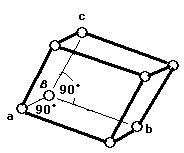
(image30) (image26)
底心単斜格子C
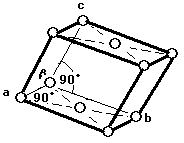体心正方格子I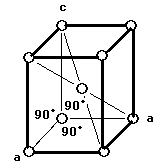 
(image27) (image28)
体心立方格子I
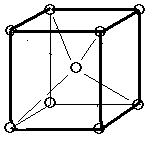面心立方格子F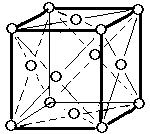 
(image22) (image24)
問2の答 39.1
ﾋﾝﾄ
● (II)の(a)から容器の体積Vは, 気体の状態方程式PV = nRTを使うと次式が成立する。
(1.00×105)×V = (42/28)×(0.0831×105)×273
よって, V = 34.03 L(ﾘｯﾄﾙ)
元素Aの原子量をAとすると
4.06×105×34.03 = (7.82/A + 42/28)×(0.0831×105)×980
(7.82/A + 1.50) = 1.70
A = 39.1
(別解)
気体定数Rが明確でない場合は
(1.00×105)×V = (42/28)×R×273
よって, V = 409.5×10-5R L(ﾘｯﾄﾙ)
4.06×105×409.5×10-5R = (7.82/A + 42/28)×R×980
(7.82/A + 1.50) = 1.70
A = 39.1
● 1atm = 101325 Pa = 760 mmHg
問3の答 42.4 cm3
ﾋﾝﾄ
(II)の(c)から物質Aの単位格子は体心立方格子である(問1の答参照)。
したがって, 体心立方格子の一辺を a [cm]とすると問1の答の図より次式が成立する
(a2 + a2) + a2 = (2×4.50×10-8)2
よって,
a = 5.20×10-8cm
単位格子の体積は…この体積内に原子Aが2個存在する,
a3 = 141×10-24 cm3
1mol の体積は
(141×10-24)/2×(6.02×10-23) = 42.4 cm3
問4の答
(3) 水と塩素との両方に反応する。
(5) 光沢があり, 熱や電気をよく通し, 密度は小さい値を示す。
ﾋﾝﾄ
● 典型金属元素の原子の基底状態の電子は, 内殻では希ｶﾞｽの安定な電子配置で最外殻に価電子が存在する。価電子は同周期で原子番号増加とともに1個ずつ増加する。
熱・電気の良伝導性, 金属光沢, 展性・延性に富む。
電気陰性度は周期表の左下ほど小さくなり陽ｲｵﾝになりやすい…還元性。
主としてｲｵﾝ結合するが共有結合性も存在する。
非金属元素との境界近くにあるものは両性が見られる。