a の答
元素 ： 銅 電子配置 ： 1s22s22p63s23p63d104s1 ブロック ： d
元素 ： ガリウム 電子配置 ： 1s22s22p63s23p63d104p24s1 ブロック ： s
元素 ： リン 電子配置 ： 1s22s22p63s23p3 ブロック ： p
● s-ブロックの元素は ns1(1族) か又は ns2(2族) のいずれかの原子価-殻の電子構造(配置)を持つ。s-ブロック元素は周期表の1族と2族に含まれる金属から成る。
これらの2つの族はそれにある元素がns1(1族)またはns2(2族)のいずれかの原子価−殻電子構造をもつのでsブロックとして引用される。1族はリチウムからフランシウムまでの元素を含み, そして2族はベリリウムからラジウムの元素を含む。ほとんどの他の金属と比較して, s-ブロックの元素は一般により大きな化学的活性をもつ。
1族と2族の金属 ： 共通性
1族元素は金属の特性を示す ： フレッシュな切断表面は光沢で, 電気と熱の伝導性が高く, 元素は延性と展性である。原子価殻中にちょうど 1個の電子の存在はこれらの元素にM+イオンを含む化合物を形成するように誘導する。
2族の元素はベリリウムは異常性を示すけれども, 同様に金属の典型的な性質を示す。原子価殻には2つの電子が存在し, そこでマグネシウムからバリウムまでのその電子はM2+イオンを含む化合物を形成する。
歴史上の理由で, 1族と2族の元素は時によってそれぞれアルカリ金属とアルカリ土類金属として知られている。
s-ブロック金属の抽出
s-ブロック金属は溶融塩の電気分解によって抽出される。
p ブロックは周期表で13族から17族までにある全ての元素を含んでいる。例えば, 3周期のp-ブロック元素はアルミニウム, ケイ素, リン, 硫黄, および塩素である。それらは非常に活性な非金属から穏やかな性質の金属まで, 非常に幅広い性質を示す。しかしながら, この全ての多様性の中で共通のパターンが存在する。
13族から17族までのp-ブロック元素全ての元素の電子構造は希ガス類似の充満した外殻と不完全な p 副殻の電子構造に対応している。例えば, ケイ素 (周期3, 14族) の電子構造は [Ne]3s23p2 である。加えて, 周期4と5のp-ブロックの元素は d 副殻をもつ, すなわち, ゲルマニウム Ge は [Ar]3d104s24p2 である。また周期6のp-ブロック元素は完全な f 副殻をもつ, すなわち, 鉛 Pb は [Xe]4f145d106s26p2 である。
注意する2つの点は最外殻の軌道は p 軌道であること, s と p の電子の全数は(族の数 - 10) に等しいことである。例えば, 上で挙げられた3つの元素の電子構造は全てが ns2np2 で終わっている。それ故これらの元素の各々のnsとnpの電子数は4で, いわゆる 14 - 10 = 4 である。
14族の元素は, 非金属 (炭素) から金属 (鉛)で, 性質に最も大きな変化を示す。
● d ブロックの遷移金属は周期 4, 5, 6 の中の周期表の中央部分を占めている。5つのd軌道のセットは各周期のコースにおいて全体で 10電子で満たされる。3d副殻は 1個から 10個までスムーズに電子で満たされることが予期される。しかし, その充満はこの予期される配列には従わない2つの場所が存在する。クロムは電子構造が 3d54s1 で 3d44s2 ではない ； そして銅は電子構造が 3d104s1 で 3d94s2 ではない。
d ブロックの最初の列 (4周期) ： スカンジウムから亜鉛まである。
カルシウムは周期4においてスカンジウムの直前の金属である。d ブロックの最初の列の全元素はカルシウムよりもより大きな第1イオン化エネルギーを持つ。
原子半径とイオン化エネルギーの両方とも, チタンTi から銅Cuまでは似た値を持つ。
原子の大きさは, 周期 2と3では原子番号にそって減少するがその理由はその増加する核電荷が外殻軌道中の電子をより強く引き付けるからである。
しかし, d ブロックのこの最初の列(周期4)では, 原子の大きさはわずかに変化するだけである。これは内部のd軌道の電子が核の電荷を遮蔽し外殻4s電子の吸引を弱めるためである。第1イオン化エネルギーもまた周期にそって僅かしか変化しないがその理由は外殻4s電子が核の電荷からよく遮蔽されているからである。
原子半径はカルシウムからクロムまでシャープに減少し, その後変化が少なくなる。
第1イオン化エネルギーはその d ブロックにそってむしろ穏やかな増加を示し, 銅から亜鉛でシャープな増加になる。
電子構造
3d 軌道は原子番号が Ti から Cu まで増加するにつれ満たされていく。そのとき電子構造の配列に注意することが必要である。
3d の副殻は電子を 1 から 10 までスムーズに充満することが予期されるが, しかし, その充満は予期される配列に従わない2つの場所が存在する。クロムは電子構造 3d54s1 を持ち 3d44s2 ではない ； 銅は電子構造 3d104s1 をもち 3d94s2 ではない。
このことは 3d と 4s の軌道はエネルギーにおいて僅かに 4s が低いがほとんど差がないという理由による； 電子が周期にそって追加されていくとき, クロムではd軌道に対して半充満であることがエネルギー的に安定し； これはフントの規則に一致し, その5つの電子は不対スピンを保持する。銅では不対電子での4s軌道を残したままで, d軌道を完全に電子対で満たすことがエネルギー的に安定となる。
b の答
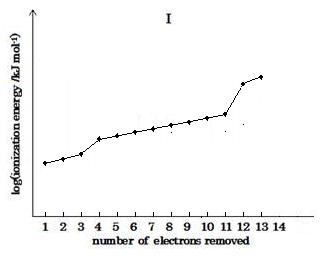(image605)グラフは段階的な増加を示すと共に3番目と4番目, および11番目と12番目の電子間に急な上昇がある。
この現象は次のように説明される即ちそのイオン化エネルギーの増加は除去される電子が核の吸引電荷に近い新殻 (4番目のL殻または12番目のK殻) から引き抜かれるときに生じる。
Al の電子構造は
Al ： 1s22s22p63s23p1
である。軌道のそのイオン化エネルギーは順序において次のように示される ；
1s<2s<2p<3s<3p
イオン化エネルギーは気相の孤立原子から電子を除くに要する最小のエネルギーである。Al では次のように表わされる ：
Al → Aln+ + ne-
そこで, 大きなエネルギーが孤立したAl原子に与えられると, 最初に, その 3p1 軌道の 1つの電子はより容易いに除かれるがその理由は他の電子よりも核から最も離れた副殻にあるからである (即ち, その 3p1 軌道のイオン化エネルギーが最も小さい値を持つ)。さらに, イオン化に対して Al にエネルギーを継続して加えると, Al中の各電子はイオン化エネルギーの増加で外殻からそれぞれ段階的にフリーになる。
3番目と4番目の電子を除去する間に必要とするエネルギーの顕著な増加が存在し, そしてもう１つの顕著な増加が 11番目と 12番目の電子の間にある。これらの現象は次のことが想定される, 即ちイオン化エネルギーの増加は除去される電子が核の吸引電荷により接近した, 新たな殻から引き抜かれねばならないときに生じる。
そのグラフは段階的な増加を示すと共に3番目と4番目, および11番目と12番目の電子間に急な上昇がある。
原子の大きさの影響
原子の大きさはそのイオンエネルギー化エネルギーに影響を及ぼし, そのエネルギーとは1個またはそれ以上の最外殻電子を除くのに必要とする最小限度のエネルギーである。同時に, そのイオン化エネルギーは酸化数として表わされる元素の原子価に影響する。これらの3つの連結された値−原子の大きさ, イオン化エネルギー, そして酸化数−の全ては原子番号での電子が周期にそって増加するときにはっきりとした傾向を示す。
原子半径の大きさ
周期表の各周期において, 1族の金属は外側に1個の原子価電子を持ち充満した内部殻は核電荷からその電子を部分的に遮蔽している。周期2と3においては, 原子半径は原子番号が1族から17族まで増加するにつれ段階的に減少する。核電荷のその段階的増加は全ての電子を核の方へより接近するように引っ張る。周期4では, 先の2つの周期に見られた傾向は内部の3d副殻が充満しているd-ブロック元素のために少しなめらかでなくなる。
遮蔽
周期にそっての継続する元素の各々は 1個以上の陽子と電子を含む。余分の電子はその余分の陽子を遮蔽することが (その陽子の引力を相殺することが) 予期される。この遮蔽は部分的にのみ影響し ； 電子密度はぼやけており, 一方陽子は核の中に明確に極在化されている。
この不完全な遮蔽は次のことを意味する, すなわち1個の電子によって試される実質的核電荷は周期にそって増加し ； その核電荷の増加は同じ殻内の過剰電子の効果よりも勝る。
第1イオン化エネルギー
原子の大きさは周期にそって原子番号が増加するにつれ減少する。それゆえ原子価電子が核により近ずくにつれ第1イオン化エネルギーを増加させることが予期されることは当然である。このことは本当である一方, 族13と16での下降に注目すべき他の2つの関心点が存在する。
第1イオン化エネルギーは ：
E(g) → E+(g) + e-(g)
のように一般の元素 E に対して表わされ, ガス状の孤立原子から 1個の電子を除くのに要請される最小限のエネルギーである。
13族/16族の下降
周期2と3において, 13族元素/16族元素でプロットの小さな下降が存在する。ベリリウム/ホウ素 (周期2) でのその下降は電子副殻によるものである確証を用意する。周期3では, アルミニウムと硫黄の第1イオン化エネルギーが予期されるよりも低い。Ma/Al の場合, Al 中の除去される電子は3p副殻からであり, それはMg から除去される3s電子よりも核からより離れている。それゆえイオン化で電子を除去するのに少ないエネルギーで済む。元素P/Sの場合では, リンの中の3p電子3個が全て隔離の3p軌道を1個ずつ占めておりそれ故電子間の反発力は小さい。一方, 硫黄では4番目のp電子によって電子間で反発力が生じておりそれだけイオン化エネルギーが小さくなる。
c の答
元素 ： ナトリウム
結晶の名称 ： 体心立方格子
配位数 ： 8
元素 ： マグネシウム
結晶の名称 ： 六方最密構造
配位数 ： 12
単純立体格子
単純立方格子は正方形の層が他の頂点に正確に置かれているときに生じる。その層は配置AAA…でくり返される。これは次のことを意味する, すなわち二層, 三層にある球状のイオンが正確に一層の同じ位置に存在する。この配列は最小の空間占有率を可能にすることを表わしている。
ある１つのイオンの配位数はその最も近い隣接イオン数を与える。単純立体結晶格子の配位数は各イオンが6つの最も近い隣接イオンを保持しているので6である。単純立体格子の唯一の金属はポロ二ウムである。
体心立方格子
各正方層の中のイオンはすぐ下の層の中のイオン間の穴へ適合するように配列するようにすることができる。そのとき正方層は二者択一的な配列 ABAB…で存在する。(これは 1, 3, 5 の中のイオンが正確に同じ相対位置に存在するが, 2, 4, 6 の層のものとは異なっていることを意味する。) これは空間のより効率的占有である (単純立方での 52%だけと比較して空間の68%が満たされている)。配位数は8で単位格子は体心立方 (b.c.c.) として記述される。 I族の金属は体心立方格子に採り入れられ, そしてそれらの小さい密度は, 他の密な充填と比較して, b.c.c.格子の相対でのすき間形成に影響を及ぼしている。
六方最密充填構造
六方の層は二者択一での順序 ABAB…において相互に積み重なっている。(層AとBはいま六方の層で参照していることに注意。) 配位数は12であり, 可能な空間の最効率占有を表わしており (空間の74%が充満している)。単位格子は六方最密充填 (h.c.p.) 構造と呼ばれている。
マグネシウム, 亜鉛, そしてチタンが固体状態で六方最密充填構造に取り上げられる一般的金属の範疇にある。
六方最密充填構造 - ABABで積み上げられた六方の層を示す。その層は異なった色で分けられておりその結果配列を見分けるのが容易である, ただし全ての球は同一である。
図(省略)
(層2の中のイオンは層1の中のイオン間の穴に存在する。層3の中のイオンは層1の中のイオン上に直接存在している。 単位格子の空間充填模型。 単位格子のボールと棒による模型。)
立体最密格子
六方層が共に積み重なることができるもう一つの仕方がある。層1と同じ状態である層3に代わって, それは最初の2層の両方の穴上に合うようにすることができる。この構造は結果として配列が ABCABC…のようになる。空間の占有率は六方最密構造 (74%) と同じで配位数はまた 12 である。この単位格子は立方最密構造と呼ばれるが, また面心立方 (f.c.c.) として記述される。この二者択一での名称を理解する最もよい方法は最密で充填されている面から眺めてみることである。立方の各々の角に球が存在しそしてまた各面の中心に球が存在する。アルミニウム, 銅, 銀, および金が固体状態で立方最密構造に適合するありふれた金属の範疇にある。
立方最密構造 - ABCABC…で積み上げられた六方の層を示している。再びその層が異なった色で表わされておりその結果として配列を見るのが容易であるが, ただし全ての球は同一である。
図(省略)
(層2のイオンは層1のイオン間の穴に位置する。層3のイオンは層1と2の穴上に位置している。 単位格子の空間充填模型。 単位格子のボールと棒による模型。)
まとめ
● 正方層は AAA…の積み上げで単純立方構造を形成する又は ABCABC…で立方最密構造を形成する。
● 六方層は ABAB…の積み上げで六方最密構造か又は ABCABC…で立方最密構造を形成する。
● 立方最密充填はまた面心立方と呼ばれる。