答　 　 　　　　　　　　　　　　元の問題へ


問1の答　　　　1.4×10²


●1　熱化学方程式 (1) を参照すると,

　　　　　　　　　　　　　　　　H₂(気) + (1/2)O₂(気) = H₂O(液) + 286 kJ　…(1)

　1 mol の H₂(気) は, 燃焼すると, 286 kJ の熱エネルギーを発生することが分かる。

●2　1 mol の H₂(気) の質量は, 原子量を用いると,

　　　　　　　　　　　　　　　　　　　　　　　　　1.0×2 = 2 g/mol

　●1 と●2 から, 水素ガスの質量 1 g 当りの燃焼エネルギーを X kJ とすると次式が成立する。

　　　　　　　　　　　　　　　　　　　　(1 g) ： (X kJ) = (2 g) ： (286 kJ)

　よって,

　　　　　　　　　　　　　　　　　　　X = 286/2 = 143 = 1.4×10² (有効数字2桁)


問2の答　　　1.2×10²

　一致しない。

　[理由]　水の状態が結合エネルギーでの反応熱では気体, 式(1)では液体で違うためである。


●1　水素燃焼の反応式は, 反応に関わる物質を全て気体状すると,

　　　　　　　　　　　　　　　　　　　　　H₂(気) + (1/2)O₂(気) → H₂O(気)

　この反応に関わる各物質のモル当りの結合エネルギーを, 水素 H-H で X kJ, 酸素 O=O で Y kJ, 水酸基 H-O で Z kJ とし, 発生する反応熱を Q kJ とすると, 近似的に次式が成立する。

　　　　　　　　　　　　　　　　　　　　　 　　Q = 2Z - {X + (1/2)Y}

　上式へ, [問題]で与えられた各結合エネルギーの値を代入すると,

　　　　　　　　　　　　　　　　　　　　Q = 2×463 - {436 + (1/2)×496} = 242

　したがって, 水素 1 g 当りの発生する熱エネルギーの値は

　　　　　　　　　　　　　　　　　　　　(1/2)×242 = 121 = 1.2×10² (有効数字2桁)


●2　一方, 熱化学方程式 (1) を参照して, 水素燃焼の反応式を考えると,

　　　　　　　　　　　　　　　　　　　　H₂(気) + (1/2)O₂(気) → H₂O(液)

　発生する反応熱を Q kJ とすると, Q = 286 となる。したがって, 水素 1 g 当りの発生する熱エネルギーは, 問1の解説のように, 143 となる。

●3　反応熱Qにおいて, ●1の場合と●2の場合を比較すると, 一致しない。この一致しない主なる理由は, 生成される水の状態が, ●1では気体, ●2では液体となっており, 水の状態が異なっているためである。


問3の答 　　　　56 kJ


●1　CH₄ ガスと水蒸気 H₂O の反応からの水素ガス製造の熱化学方程式 (2) は

　　　　　　　　　　　　　　　　　CH₄(気) + 2H₂O(気) = 4H₂(気) + CO₂(気) - 165 kJ　…(2)

●2　水の蒸発熱の熱化学方程式は

　　　　　　　　　　　　　　　　　　　　　　H₂O(液) = H₂O(気) - 44 kJ

●3　CH₄ ガスと液体 H₂O の反応からの水素ガス製造の熱化学方程式は, その反応熱を Q kJ とすると,

　　　　　　　　　　　　　　　　　　　CH₄(気) + 2H₂O(液) = 4H₂(気) + CO₂(気) + Q kJ

　●1と●2の式を使用すると, 反応熱 Q は

　　Q = {CH₄(気) + 2H₂O(液)} - {4H₂(気) + CO₂(気)}

　　　 = [{4H₂(気) + CO₂(気) - 165 kJ - 2H₂O(気)} + 2{H₂O(気) - 44 kJ}] - {4H₂(気) + CO₂(気)}

　　　 = - 165 kJ - 2×44 kJ = -253 kJ

　よって, CH₄ ガスと液体 H₂O の反応からの水素ガス製造の熱化学方程式は

　　　　　　　　　　　　　　　　　　CH₄(気) + 2H₂O(液) = 4H₂(気) + CO₂(気) - 253 kJ

　発生水素は 4 mol なので, 4 mol の水素ガスの燃焼熱は, [問題]文中の熱化学方程式 (1) を参照すると

　　　　　　　　　　　　　　　　　　4 mol の水素ガスの燃焼熱 = 4×286 kJ = 1144 kJ

　したがって, 1 mol のメタンガス燃焼においては, 実質の発生熱は

　　　　　　　　　　　　　　　　　　　　　　　　1144 kJ - 253 kJ = 891 kJ

　1 g 当りでは, メタン CH₄ の分子量は 1×12.0 + 4×1.0 = 16.0 なので

　　　　　　　　　　　　　　　　　　891 kJ/(16 g) = 55.6875 = 56 kJ・g^-1 (有効数字2桁)


問4の答　　　H 原子

　[理由]　Hの1s電子と比べるとLiの2s電子は原子核との距離が大きいのでH原子の方へクーロン力で近づく。


●　Li と H の電子配置において,

　　　　　　　　　　　　　　　　　　　　　　　　　　　Li ： 1s²2s¹

　　　　　　　　　　　　　　　　　　　　　　　　　　　H ： 1s¹

　ここで, K殻に存在する H の1s電子と比較すると, L殻に存在する Li の最外殻の2s電子は, Li 原子核からの距離が大きい。したがって, Li 原子と H 原子とが近接すると, その間に存在する Li 原子の最外殻の 2s電子は H原子の方へクーロン力で引きよせられ, 負電荷はH原子の方へ偏る。結果として, 形成された固体 LiH 中の結合はイオン性の共有結合となる。


問5の答　　　9.6

　　　　　　　　　　　　　　　　　　　　　

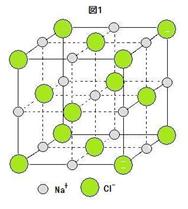
　図1を参照して, Cl^- の中心を Li の中心, Na⁺ の中心を H の中心とすると, この立方体の結晶構造内において,

●1　Li 原子数は次のようになる。

　　　　　　　　　　　　　　　　　　　　立方体の角 ： 8×(1/8) = 1個

　　　　　　　　　　　　　　　　　　　　立方体の面心 ： 6×(1/2) = 3個

　　　　　　　　　　　　　　　　　　　　よって, 合計 4個

●2　H 原子数は次のようになる。

　　　　　　　　　　　　　　　　　　　　立方体の稜 ： 12×(1/4) = 3個

　　　　　　　　　　　　　　　　　　　　立方体の中心 ： 1個

　　　　　　　　　　　　　　　　　　　　よって, 合計 4個

●3　立方体の体積 V は

　　　　　　　　　　　V = (2×0.2 nm)³ = (0.4×10^-7 cm)³ = 0.064×10^-21 cm³ = 6.4×10^-23 ml

　以上から, この体積 6.4×10^-23 ml 中に, H原子は 4個存在し, その質量は (4 g)/(6.0×10²³) であるから, 水素 1 g 当りの体積を X ml とすると, 次の比例式が成立する。

　　　　　　　　　　　　　　　　　　　　1 ： X = 4/(6.0×10²³) ： 6.4×10^-23

　　　　　　　　　　　　　　　　　　　　1 ： X = 0.67×10^-23 ：　6.4×10^-23

　よって,

　　　　　　　　　　　　　　　　　　 　　　　　X = 9.6 (有効数字2桁)