問1の答
(ア. 1) (合成) (多糖類) (タンパク質) (天然ゴム)
●下図(image145)の構造は, I:アミロース(α-グルコースが直鎖状に結合。A:点線四角内はα-1,4-グリコシド結合部を表す), II:セルロース(β-グルコースが直鎖状に結合。B:点線四角内はβ-1,4-グリコシド結合部を表す), III:アミロペクチンとグリコーゲン(α-グルコースが直鎖状に結合し, さらにα-1,6-グリコシド結合により枝分かれする。C:点線四角内はα-1,6-グリコシド結合部を表す)…動物の肝臓や筋肉に蓄えられるグリコーゲンはアミロペクチンよりも枝分かれが多い。
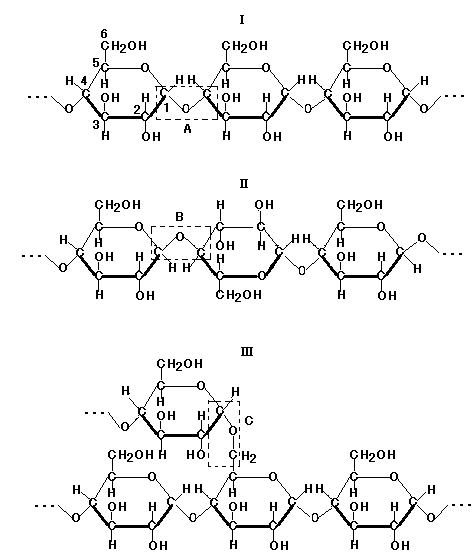
デンプンは希硫酸溶液中で長時間放置しておくと完全に加水分解して単糖類のグルコースになる。平衡状態では次の図(image146)のように3種のα-グルコース…IV, アルデヒド型グルコース…V, β-グルコース…VIが存在する。アルデヒド型グルコースには分子中にアルデヒド基が存在し還元性を示す。

●[平均分子量]…高分子の分子量は単一ではなく種々の分子量をもつ分子の混合物である。どんなに分別しても単一分子量の試料を得ることはできない。したがって, 高分子には分子量分布曲線が存在する。
高分子の分子量は平均分子量が用いられる。ふつう高分子の分子量は次式の数平均分子量を意味する:
高分子の数平均分子量 = (ΣMiNi)/(ΣNi) ただし, Mi:i分子の分子量, Ni:i分子の数
数平均分子量以外に, 重量平均分子量, Z平均分子量(超遠心機使用), 粘度平均分子量などがある。
問2
(1)の答 A:セルロース
[理由] セルロースはβ-グルコースがβ-1,4-グリコシド結合によって直鎖状に結合した多糖類で, 分子内にはα-1,4-グリコシド結合が存在しない。したがって, 酵素によって加水分解されず銀鏡反応を示さない。
一方, 他の多糖類のアミロース, アミロペクチン, グリコーゲンはα-1,4-グリコシド結合が存在するので酵素によって加水分解されて単糖類のグルコースを生じ, 還元性のアルデヒド型グルコースが銀鏡反応を示す。
(2)の答 CとD:アミロペクチンとグリコーゲン
[理由] α-1,6-グリコシド結合のみを加水分解する酵素は, α-1,6-グリコシド結合が存在するアミロペクチンと グリコーゲンに作用してα-1,6-グリコシド結合を切断する。
α-1,6-グリコシド結合の切断で生じた糖類の一部は還元性のアルデヒド基を持つので, フェーリング溶液と反応して赤色の酸化銅(I)沈殿を生成する。
(3)の答 D:グリコーゲン
[理由] Dのグリコーゲン分子はα-1,6-グリコシド結合によって多く枝分かれしている。したがって, α-1,6-グリコシド結合のみを加水分解する酵素を加え十分反応させると, 分子はばらばらに切断され,分子量の小さい糖類になる。多くの分子量の小さい糖類は半透膜を透して流水へ放出され, 半透膜内の糖類の質量は軽くなる。
B:アミロース C:アミロペクチン
●解答の手順
[実験2]から, 酵素分解するのはCとDで, アミロペクチンとグリコーゲンのいずれかに相当する。 AとBは酵素分解をしない。したがって, Aは既に解答(1)からセルローに決定しているので, Bはアミロースになる。
[実験3]で, 酵素分解の生成物の質量がもっとも軽いことから, Dが多く枝分かれしていることになる。これよりDはグリコーゲンに相当し, [実験2]を考慮してCがアミロペクチンに相当する。
(4)の答(image266)
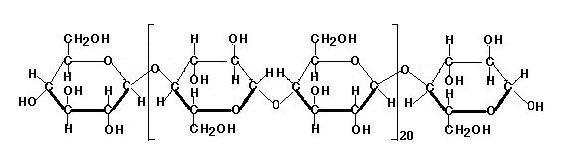
A水溶液に含まれる溶質:セルロースの燃焼を例の構造式の上で考えると, その完全燃焼の反応式は次のようになる。
C6H11O6-[C12H20O10]n-C6H11O5 + 12(n + 1)O2 → 12(n + 1)CO2 + (10n + 11)H2O …①
水の物質量mol は, 5の塩化カルシウムは発生した水蒸気を吸収して質量が 0.093g 増加したことから,
0.093/18 = 0.0051667 mol …②
二酸化炭素の物質量mol は, 6のソーダ石灰は発生した二酸化炭素を吸収して質量が1.848g 増加したことから,
1.848/44 = 0.042 mol …③
セルロースの物質量 mol は, 分子量が 324n + 342 から
1.137/(324n + 342) mol …④
セルロースと二酸化炭素の mol 比は, ①, ③, ④から次式になる。
1.137/(324n + 342) : 0.042 = 1 : 12(n + 1) …⑤
よって, ⑤から
1.137×12(n + 1)/(324n + 342) = 0.042
0.042(324n + 342) = 13.644(n + 1)
13.644n - 13.608n = 14.364 - 13.644
n = 20